Zadanie 3 - Pole Grawitacyjne - orbita geostacjonarna

Orbita geostacjonarna a więc taka na jakiej ciało będzie się znajdować cały czas nad tym samym miejscem nad powierzchnią Ziemi.

Muszą być spełnione warunki:

T=T_{Ziemi}=24h=86400s

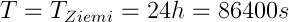
A więc okres obiegu tego ciała musi być równy okresowi obiegu Ziemi - jednej dobie.

Oraz:

F_{d}=F_{g}

A więc siła odśrodkowa działająca na obracające się po orbicie geostacjonarnej ciało musi być równa sile grawitacji. Rozpisując ten warunek mamy:

\frac{mv^2}{R}=G\frac{Mm}{R^2}

Gdzie R jest promieniem orbity geostacjonarnej a więc jest równy sumie długości promienia Ziemi „Rz” i wysokości „H” – która jest odległością orbity geostacjonarnej od powierzchni Ziemi i jednocześnie to właśnie ją mamy policzyć. Zapisać więc można:

R=R_{z}+H

Dodatkowo musimy wiedzieć też coś o prędkości z jaką porusza się na orbicie geostacjonarnej dowolne ciało, dzięki temu, że znamy okres obiegu, zadanie stanie się teraz w pełni wykonywalne.

v=\frac{2\pi R}{T}


Mamy szereg wniosków, teraz wystarczy dokonać prostych przekształceń.


Zaczniemy od równowagi sił, bo to dla nas najważniejsze równanie, dzielimy je przez masę „m” i jednocześnie mnożymy przez promień orbity geostacjonarnej „R”. Otrzymujemy:

v^2=\frac{GM}{R}
Podstawiamy za v.

Czyli otrzymujemy:

\frac{4 {\pi}^2 R^2}{T^2}=\frac{GM}{R}


Wypada trochę poprzekształcać, otrzymujemy:

4 {\pi}^2 R^3=GMT^2

Przekształćmy tak, aby otrzymać R, otrzymujemy:

R=\sqrt[3]{\frac{GMT^2}{4 {\pi}^2 }}


Teraz warto podstawić za R.



R_{z}+H=\sqrt[3]{\frac{GMT^2}{4 {\pi}^2 }}


I przekształcić tak aby otrzymać wysokość „H” – czyli odległość orbity geostacjonarnej od powierzchni Ziemi – szukaną wartość. Warto wstawić również M=Mz czyli masa planety której orbita geostacjonarna jest rozpatrywana jest równa masie Ziemi, gdyż planeta ta jest Ziemią jak wynika z treści zadania.



Ostatecznie otrzymujemy:

H=\sqrt[3]{\frac{GM_{z}T^2}{4 {\pi}^2 }} \; \;  - \; R _{z}


Standardowo, jeżeli są jakieś pytania prosimy o komentarze.