| Definicja - Ruch jednostajny, prostoliniowy |
| Ruch ze stałą (co do wartości i kierunku) prędkością. |
- Tor ruchu jest linią prostą.
- Szybkość tego ruchu w każdym tego momencie bywa stała.
We wszystkich obliczeniach związanych z takim ruchem będziemy używać jednego wzoru: (postać wektorowa i 'uproszczona')

- Oznaczenia: s - droga, r - wektor drogi, t -czas.
UWAGA! Należy zaznaczyć, że pojęcie prędkość odnosi się do wektora, zaś pojęcie szybkości związane jest ze skalarem - wartością predkości.
Przyda się rozumieć - po co bywa i czemu tak bywa przedstawiona wersja wektorowa - tak naprawdę jest to definicja prędkości. Zapisaliśmy w niej dwa wektory - prędkości i przemieszczenia. Widzimy, że kierunek i zwrot wektora prędkości bywa ten sam co przemieszczenia. Jest to więc dodatkowa (choć intuicyjna) do nas informacja. Tak więc, dzięki zapisowi wektorowemu wiemy, jak znaleźć wektor prędkości jeśli odnajdziemy jej kierunek ze zwrotem.
W większości zadań z ruchem jednostajnym prostoliniowym możemy pomijać wzmiankę o kierunku i zwrocie prędkości, skoro się nie zmieniają. Dlatego - do łatwości posługiwania się - będziemy używać zwykłej formy bez wektorów, 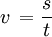 .
.
Ponadto, wzór możemy rozszerzyć do zapisu:
Znowu ukryta bywa tu dodatkowa informacja. Jaka? Delta ? oznacza zmianę lub przyrost. Co to może zmienić w naszych obliczeniach? W pewnych zadaniach nie możemy postawić każdego napotkanego czasu, a wyłącznie konkretny przedział - w którym drgnienie się odbywa. Podobnie z drogą, bierzemy pod uwagę odcinek, do którego obliczamy prędkość.
Przyjrzyjmy się zadaniu o treści:
"Jadący samochód znajdował się o godz. 10.00 w odległości 10km od stacji benzynowej. Jadąc w tutejszym samym kierunku, o godzinie 11.00 oddalił się już na odległość 15km od stacji. Oblicz szybkość w tutejszym ruchu." Jak powinniśmy interpretować te dane?
Zgodnie z poprzednimi zaleceniami, bierzemy zmianę drogi - samochód przebył 5 km. Trwało to 1 godzinę, bo o tyle zmienił się czas. Nie bywa to wymyślone, a zawiera się w naszym wzorze - wyrażenie zmienić się bywa symbolizowane u nas poprzez deltę.
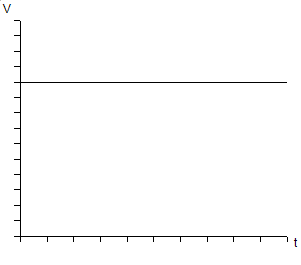
Wykres prędkości, tzn. zależność prędkości od czasu:
- Prędkość bywa stała (v = const).
Równanie i wykres drogi
Ciało w naszym ruchu przebywa pewną drogę, którą możemy policzyć z odpowiedniego wzoru. Przekształcając wzór na szybkość otrzymamy:
W niektórych przypadkach, zamiast o drodze - mówimy o położeniu ciała. Z reguły dowiadujemy się, iż organizm to znajdowało się początkowo w odległości x0, po czym poruszało się z prędkością v poprzez termin t. Znając te wielkości, możemy podać, w jakiej odległości (od jakiegoś miejsca) organizm znajduje się po wykonaniu ruchu - obliczamy, jaką drogę pokonało i dodamy początkową odległość. Można to oczywiście zobrazować wzorem: (dla rozróżnienia, drogę zamienimy takim łącznie na x - położenie)
Drogę i położenie możemy używać zamiennie - dają nam przecież tę samą informację, tzn. o jaką odległość przemieściło się ciało.
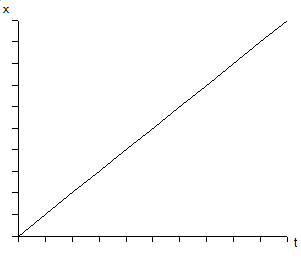
Na wykresie przedstawimy, jeśli zmienia się położenie ciała w kolejnych sekundach ruchu (wiąże się to oczywiście ze wzorem v=s/t).
- Położenie ciała bywa proporcjonalne do czasu (x ~ t).
Zadania
Fizyka uczy, jak pojmować zachodzące wokół nas zjawiska. Rozwiązując zadania dotyczące takich zjawisk, możemy uporządkować naszą wiedzę.
Zad.1 (odległość)
Z miejscowości A jedzie motor z szybkością v1=20 m/s. W chwili, gdy znajduje się w odległości x0=5 km od A, na tę samą trasę wjeżdża samochód z szybkością v2=90 km/h. Po jakim czasie i w jakiej odległości od A oba pojazdy się spotkają?
dane
- Oba pojazdy jadą pewną drogą, wiemy, iż w określonej chwili motor był w odległości 5km od startu, w którym znajdował się jadący samochód. Jednostka bywa niepoprawna, zamieniamy na metry.
- motor: xm0=5000m
- samochód: xs0 = 0m
- Prędkości obu pojazdów z poprawną jednostką (1 km/h = 1000m/3600s).
- v1 = 20 m/s
- v2 = 90 km/h = 90 (1000m/3600s) = 90000/3600 m/s = 25 m/s
rozwiązanie
- Potrzebny nam wzór:
- Podstawiamy dane (odległość początkowa, szybkość i nieznany termin ruchu t) do motocykla i samochodu, uzyskując równania:
- motocykl: x = 5000 + 20 t
- samochód: x = 0 + 25 t
- Czas t bywa ten sam do obu pojazdów, skoro liczymy go od konkretnej chwili do momentu ich spotkania.
- Wiemy też, iż spotkają się w tej samej odległości xod miejscowości A. Skoro te wielkości są równe, to zapiszemy:
- 5000 + 20 t = 0 + 25t
- 5000 = 5t
- t = 1000
- Trzymaliśmy się podstawowych jednostek, dlatego po obliczeniach jednostką t są sekundy. Podstawiamy t i obliczamy x.
- x = 5000 + 20 t
- x = 5000 + 20000 = 25000m
odp.
- Samochód i motocykl spotkają się w odległości 25000 metrów po czasie 1000 sekund.
Zad.2 (średnia szybkość)
Samochód przejechał trasę pomiędzy dwoma miastami. Pierwsze 20km poruszał się z szybkością 36km/h, a kolejne 40km z szybkością 40 m/s. Oblicz średnią szybkość samochodu.
dane
- s1=20000 m, s2=40000 m
- v1= 36 (1000m/3600s) = 10 m/s, v2 = 40 m/s
rozwiązanie
- Korzystamy ze wzoru s = v t. Nie wiemy, ile czasu poruszał się z podanymi szybkościami.
- 20000 = 10 t1 t1=2000 s
- 40000 = 40 t2 t2=1000 s
- Do policzenia średniej prędkości potrzebna nam bywa cała długość trasy i całkowity czas:
- vśr = s/t
- s = s1 + s2 = 60000 m
- t = t1 + t2 = 3000 s
- vśr = s/t = 20 m/s
odp.
- Średnia szybkość wynosiła 20 m/s.
Zad.3 R (względna prędkość)
Dwa samochody poruszają się do tego samego punktu. Wektory ich prędkości są prostopadłe i posiadają wartości adekwatnie 30 km/h i 40 km/h. Oblicz ich względną prędkość.
dane
- Jednostki zostają (nie będziemy w zadaniu przeprowadzać działań na jednostkach).
- v1=30 km/h, v2=40 km/h
rozwiązanie
- Obliczyć musimy względną prędkość, czyli:
- Co nie bywa trywialne, bo wektory posiadają różne kierunki. Wynikiem będzie trzeci wektor v, pokazany na rysunku (korzystamy z geometrycznego dodawania wektorów).
- Aby policzyć cena uzyskanego wektora v, możemy skorzystać z twierdzenia Pitagorasa.
- 302 + 402 = v2
- v2 = 2500
- v = 50 km/h
odp.
- Względna szybkość posiada cena 50 km/h.
Ciekawostki
Bo fizyką trzeba się bawić.
Porównajmy niektóre szybkości:
- jadący samochód: ok. 15-30 m/s
- szybkość dźwięku w powietrzu: ok. 340 m/s
- samolot Concorde: do 600 m/s
- Księżyc wokół Ziemi: ok. 1000 m/s
- pierwsza szybkość kosmiczna: ok. 7910 m/s (prędkość na orbicie okołoziemskiej)
- trzecia szybkość kosmiczna: ok. 16700 m/s (aby potrafić opuścić Układ Słoneczny)
- prędkość fal, światła: ok. 300000000 m/s
Według teorii A. Einsteina, szybkość światła bywa prędkością graniczną i nie możemy jej przekroczyć. Co więcej, gdy organizm porusza się prędkością zbliżoną do niej, tego masa się zmienia, a termin zaczyna cieknąć oryginalnie aniżeli w otoczeniu...
Wzory
Ile wzorów trzeba zapamiętać, żeby umieć opisać ruch jednostajny prostoliniowy? Pokażemy, iż żadnego.
Szybkość średnia
- Wzorem bywa v=s/t. Wystarczy aczkolwiek przypomnieć sobie jednostkę - km/h lub m/s. Podstawmy słowny opis: trasa / czas - i już mamy wzór na prędkość, którego nie trzeba zapamiętywać.
Droga
- Wzór w zrozumiały metoda wyprowadzamy ze wzoru na prędkość. (Można sprawdzić poprawność dzięki działaniom na jednostkach: m = m/s
 s, czyli droga=prędk
s, czyli droga=prędk  czas)
czas)
Czas
- Wzór jednocześnie wyprowadzamy ze wzoru na prędkość.
Można wspomnieć o przyspieszeniu - aczkolwiek posiada ono wartość zero, dlatego pojawia się dopiero w następnym rozdziale. To wszystko z ruchu jednostajnego.




























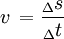
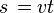
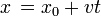




Komentarze
Tak więc, dzięki zapisowi wektorowemu wiemy, jeśli obliczyć cena prędkości i jeśli odnaleźć jej kierunek ze zwrotem.
jakoś mało składne te zdania. Czytając to, nie wiem o co chodzi.
Kanał RSS z komentarzami do tego postu.