Korepetycje
Polecane książki
|
|
Dynamika - oddziaływania podstawowe, masa, pęd, siła
Dotychczas zajmowaliśmy się wyłącznie opisem ruch (za pomocą wektorów r, v, oraz a). Były to rozważania geometryczne. Teraz omówimy przyczyny ruchu, zajmiemy się dynamiką.
Nasze rozważania ograniczymy do przypadku ciał poruszających się z małymi (w porównaniu z prędkością światła c) prędkościami tzn. zajmujemy się mechaniką klasyczną.
Żeby móc przewidzieć jaki będzie ruch ciała wywołany siłą na nie działającą trzeba wiedzieć jakiego rodzaju jest to siła i skąd się bierze. Dlatego rozpoczniemy nasze rozważania od poznania podstawowych oddziaływań oraz od zdefiniowania masy, pędu i wprowadzenia pojęcia siły F. Następnie poszukamy praw rządzących oddziaływaniami, a w dalszych częściach zajmiemy się poszczególnymi oddziaływaniami występującymi w przyrodzie.
Oddziaływania podstawowe
Według naszej dotychczasowej wiedzy istnieją tylko cztery podstawowe oddziaływania
(siły), z których wynikają wszystkie siły i oddziaływania zaobserwowane we
Wszechświecie:
- Oddziaływanie grawitacyjne - siła grawitacyjna działa na wszystkie masy (jest siłą
powszechną) i pochodzi od mas; ma długi zasięg i najmniejsze względne natężenie; - Oddziaływanie elektromagnetyczne - siła elektromagnetyczna działa na ładunki i prądy
i jej źródłem są ładunki i prądy; ma długi zasięg. Siły międzyatomowe mają charakter
elektromagnetyczny ponieważ atomy zawierają naładowane elektrony i protony,
a oddziaływania elektromagnetyczne ma wielokrotnie większe natężenie od
grawitacyjnego. Większość sił z jakimi spotykamy się na co dzień np. tarcie, siła
sprężystości jest wynikiem oddziaływania atomów, są to więc siły elektromagnetyczne; - Oddziaływanie jądrowe (silne) - siła utrzymująca w całości jądra atomowe pomimo
odpychania między protonami (ładunki dodatnie), ma bardzo krótki zasięg i największe
względne natężenie; - Oddziaływanie słabe - temu oddziaływaniu podlegają wszystkie cząstki elementarne,
w szczególności oddziaływanie to odpowiada za rozpady cząstek elementarnych.
W tabeli poniżej zestawione są cztery oddziaływania podstawowe.
| Oddziaływanie |
źródło oddziaływania |
względna siła |
Zasięg |
| Grawitacyjne | Masa | około 10-38 |
Długi |
| Elektromagnetyczne | Ładunek elektryczny |
około 10-2 |
Długi |
| Silne | m.in. protony, neutrony |
1 | Krótki (około 10-15 m) |
| Słabe | cząstki elementarne |
około 10-15 |
Krótki (około 10-18 m) |
Masa
Nasze rozważania rozpoczynamy od przypisania ciałom masy m. Chcemy w ten sposób opisać fakt, że różne ciała wykonane z tego samego materiału, w tym samym otoczeniu uzyskują pod działaniem tej samej siły różne przyspieszenia (np. pchamy z jednakową siłą dwa rożne pojazdy "lekki" i "ciężki" i uzyskują one różne a). Zaproponowana poniżej metoda postępowania jest jednym z równoważnych sposobów definiowania masy. Opiera się ona na porównaniu nieznanej masy m z wzorcem masy m0 = 1 kg. Pomiędzy masami umieszczamy ściśniętą sprężynę i następnie zwalniamy ją.
Masy m i m0, które początkowo spoczywały polecą odrzucone w przeciwnych kierunkach
odpowiednio z prędkościami v i v0 - rysunek.

Nieznaną masę m definiujemy jako
Definicja:

Jednostką masy w układzie SI jest kilogram (1kg) zdefiniowany za pomocą wzorca masy w Sevres (Francja).
Pęd
definicja:
Pęd ciała definiujemy jako iloczyn jego masy i prędkości (wektorowej)
Matematycznie można to sformułować więc tak:

Jednostką pędu jest ![[p]=1kg\cdot1\frac{m}{s} [p]=1kg\cdot1\frac{m}{s}](/images/joomlatex/5ac68dd384d2c98c02132c3b05397d93.gif) , pęd nie posiada własnej (w sensie nazwanej) jednostki.
, pęd nie posiada własnej (w sensie nazwanej) jednostki.
Siła
definicja:
Jeżeli na ciało o masie m działa siła F, to definiujemy ją jako zmianę w czasie pędu
tego ciała.
matematycznie można to zapisać tak:

w uproszczeniu (jeżeli masa ciała jest stała, m=const):

i w kolejnym uproszczeniu - jeżeli zmiana pędu jest liniowa:

Wprowadziliśmy w ten sposób pojęcie siły F. Teraz podamy metodę obliczania sił działających na ciała; poznamy prawa rządzące oddziaływaniami.
Jednostką siły jest niuton (N) - 
Jeżeli masz jakieś pytania, zachęcam do zadawania pytań w komentarzach poniżej, gwarantujemy rozwiązanie wszystkich Twoich wątpliwości.
Siła Bezwładności
Zgodnie z I zasadą dynamiki Newtona w układach inercjalnych, kiedy siły działające na ciało równoważą się pozostaje ono w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Zupełnie odmienna sytuacja zachodzi w układach nieinercjalnych, gdzie ciało przyśpiesza za sprawą przyspieszenia układu, choć nie działają na nie żadne niezrównoważone siły. Gdy układ przekazuje cialu swoje przyśpieszenie pojawia się siła kontrreakcji zwana właśnie bezwładnością. Stąd jej zwrot przeciwny jest do zwrotu przyśpieszenia układu.
Bezwładność ciał jest to ich zdolność do przeciwstawiania się wszelkim zmianom ruchu.
gdzie:
 - siła bezwładności
- siła bezwładności - przyśpieszenie układu
- przyśpieszenie układu- m - masa ciała
Wzór ten uwzględznia zwrot siły bezwładności.
Podróż windą
Dobrym przykładem ilustrującym występowanie siły bezwładności jest podróż windą. Kiedy rusza do góry z dużym przyspieszeniem czujemy się wbijani w podłogę. Z kolei gdy gwałtownie hamuje, że zaraz wzlecimy w powietrze. Podobnie jest ze zjeżdżaniem na dół. Kiedy winda zaczyna opadać, czujemy się unoszeni, zaś kiedy hamuje na dole, że "coś przyciska nas do podłogi". Dzieje się tak za sprawą działającej na nas siły bezwładności.
Analizując dane przykłady zastanówmy się jak zależy zwrot siły bezwładności od zwrotu przyspieszenia i prędkości.
W przypadku jazdy w górę:
- winda rusza - wektor przyspieszenia (ruch przyśpieszony) oraz prędkości windy skierowane ku górze, wektor bezwładności ku dołowi ("wbijanie w ziemię")
- winda hamuje - wektor przyśpieszenia windy skierowany ku dołowi (ruch opóźniony), wektor prędkości windy skierowany ku górze (bo winda mimo wszystko jedzie do góry), wektor siły bezwładności ku górze ("odrywamy się od podłogi")
Na tych dwóch przykładać widać już wyraźnie, że wektor prędkości nie wpływa na zwrot siły bezwładności. Wszak w obu przypadkach skierowany był ku górze, a zwrot siły bezwładności zmieniał się. Jasno dostrzegalny jest za to związek między zwrotem przyspieszenia a zwrotem siły bezwładności.
Siła bezwładności działa przeciwnie do zwrotu przyśpieszenia
W ramach powtórzenia i lepszego zrozumienia zagadnienia spróbuj samodzielnie przeanalizować zwroty prędkości, przyśpieszenia i siły bezwładności podczas jazdy w dól.
Sily pozorne
Jak już mówiliśmy we wstępie siła bezwładności ściśle związana jest z układami nieinercjalnymi - takimi, w których ciało przyśpiesza ponieważ przyśpiesza jego układ.
Gdy stojący samochód gwałtownie zaczyna się poruszać czujemy się wbijani w oparcie fotela. Jednak raz wprawiona w ruch maszyna poruszająca się ruchem jednostajnym nie wywołuje już takich reakcji. Dlaczego? Dzieje się tak ponieważ w pierwszym przypadku znajdujemy się w układzie odniesienia posiadającym własne przyśpieszenie, a co za tym idzie nadającym nam siłę pozorną. Gdy układ przekazuje nam swoje przyśpieszenie pojawia się siła bezwładności - kontrreakcji. Stąd jest ona skierowana przeciwnie do zwrotu przyśpieszenia układu.
Do sił pozornych należy nie tylko bezwładność ale też siły odśrodkowa i dośrodkowa występujące gdy ciało porusza się po łuku. Ruch po okręgu należy do układów nieinercjalnych, gdyż występuje w nim przyśpieszenie dośrodkowe.
Efekt Coriolisa
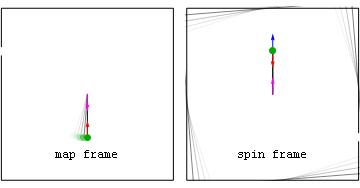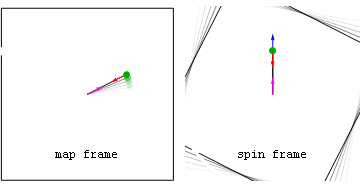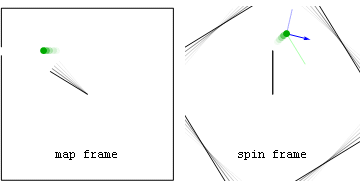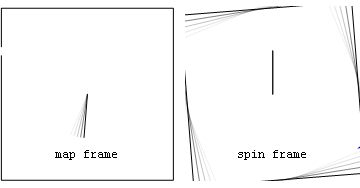
Efekt Coriolisa podobnie jak siła bezwładności działa jedynie w układach nieinercjalnych. Dla obserwatora znajdującego się w obracającym się układzie odniesienia tor ruchu ciał znajdującego się w tym samym układzie jest zakrzywiony. Dzieje się tak za sprawą pozornej siły Corolisa.
Pierwsza ramka przedstawia obiekt z perspektywy osoby pozostającej w bezruchu. W drugim przypadku uklad ukazany jest oczyma obserwatora znajdującego się w obracającym się układzie.
Siły w ruchu po okręgu
Działające na ciało poruszające się po łuku siły odśrodkowa i dośrodkowa są siłami bezwładności, więc również należą do sił pozornych. 
Do zrobienia:
|

 Wyświetlenie artykułów z etykietą: siła
Wyświetlenie artykułów z etykietą: siła