Fizyka jądrowa - Zadanie 2 - rozpad promieniotwórczy - Fizyka Dla Każdego

wtorek, 22 lutego 2011 02:32

Fizyka jądrowa - Zadanie 2 - rozpad promieniotwórczy

Napisał dr inż. Paweł Troka

Oceń ten artykuł

(2 głosów)

W czasie 10 godzin 75% początkowej liczby jąder uległo rozpadowi. Ile Wynosi czas połowicznego zaniku?

Kliknij "więcej" aby zobaczyć rozwiązanie

Pamiętajmy, że mamy obszerne dane:

t=10h

$N_{k}=(1-0,75) \cdot N_{0}=\frac{1}{4}N_{0}$

T=?

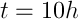
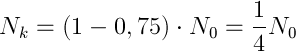
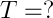
Podstawowy wzór z jakiego musimy skorzystać to wzór opisujący zależność ilości atomów pierwiastka promieniotwórczego od czasu:

$N(t)=N_{0} \cdot (\frac{1}{2})^{\frac{t}{T}}$		[1]

Nasz czas jest równy t=10h a mamy policzyć T, czyli okres połowicznego rozpadu (czy inaczej czas potrzebny do zaniku połowy jąder pierwiastka).

Wiemy że:

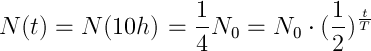$N(t)=N(10h)=\frac{1}{4}N_0=N_{0} \cdot (\frac{1}{2})^{\frac{t}{T}}$		[2]

Teraz wystarczy przekształcić wzór, tak aby otrzymać T:

$\frac{\frac{1}{4}N_0}{N_0}=(\frac{1}{2})^{\frac{t}{T}}$

$(\frac{1}{2})^{\frac{t}{T}}=\frac{1}{4}$

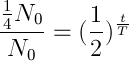
Nie musimy nawet używać logarytmów, gdyż z powyższego od razu widać że:

${\frac{t}{T}}=2$

${\frac{t}{2}}=T$

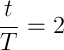
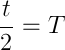
Teraz wystarczy podstawić dane:

$T={\frac{t}{2}}={\frac{10h}{2}}=5h$

T=5h

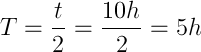
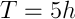
A więc znamy odpowiedź, czas połowicznego zaniku wynosi 5h.

Gdyby były jakieś pytania, standardowo komentujcie ;)

Czytany 13879 razy Ostatnio zmieniany poniedziałek, 22 sierpnia 2011 21:19

Podziel się tym z innymi

Owner & CEO
E-Mail: ptroka@fizyka.dk
PTroka on Google+

Strona: fizyka.dk