Fizyka

Teoria

Kinematyka

Ruch przyśpieszony

Korepetycje

Znajdź korepetytora!

Polecane książki

piątek, 26 listopada 2010 23:43

Ruch przyśpieszony

Napisał dr inż. Paweł Troka

wielkość czcionki zmniejsz wielkość czcionki powiększ czcionkę
Wydrukuj
Email
Comments (3)

Oceń ten artykuł

(5 głosów)

Ruch jednostajnie przyśpieszony

Zaczniemy od opisania ruchu startującego samolotu. Prześledźmy sytuację: na początku samolot spoczywa, po pierwszej sekundzie może posiadać szybkość 1m/s, w drugiej osiągnie 2m/s, w trzeciej szybkość będzie równa 3m/s. Po minucie może ruszać się z prędkością np. 60m/s.

Nie wygląda to na drgnienie ze stałą prędkością. Mimo to, opisanie go nie stanowi do nas problemu - wystarczy przyjąć nową wielkość, którą bywa przyspieszenie, symbol a. Określać będzie, jeśli zmienia się prędkość. Jeśli w ruchu występuje przyspieszenie, wówczas szybkość v zmienia się w każdej sekundzie o cena a. Dzieląc prędkość, którą uzyskało ciało, poprzez długość trwania ruchu, otrzymamy przyspieszenie: $a=\frac{v}{t}\,$ .

Oczywiście, nie weźmiemy przypadkowej prędkości - interesuje nas zmiana prędkości w odpowiednim przedziale czasu. Przekładając to na 'wzory', otrzymamy:

$a=\frac{_{\Delta}v}{t}$

Przykład
Pociąg jadący z prędkością 10m/s poprzez 60 sekund przyspieszał tak, iż osiągnął szybkość 25m/s. Jak tego przyspieszenie posiada się do przyspieszenia samochodu, jaki od 0 do 100km/h rozpędzi się w 14 sekund?

Opiszmy pociąg:

zmiana prędkości i czas: $_{\Delta}v=25-10=15 \,\mbox{m/s}, \quad t = 60 \,s$

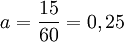
obliczmy przyspieszenie: $a = \frac{15}{60}= 0,25$

Z jaką jednostką podamy wynik? Według działań: szybkość (m/s) dzieli się poprzez termin (s), z tego również otrzymujemy: $\frac{\mbox{m}}{\mbox{s}^2}$ .

Opiszmy samochód:

zmiana prędkości: 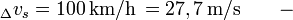$_{\Delta}v_s = 100\, \mbox{km/h} \,= 27,7\, \mbox{m/s} \qquad -$ interesują nas wyłącznie [m/s]

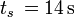
czas: $t_s \,= 14 \,\mbox{s}$

przyspieszenie: $a_s = \frac{27,7}{14} = 1,98 \; \frac{\mbox{m}}{\mbox{s}^2}$

Przyspieszenie pociągu wynosiło 0,25, natomiast przyspieszenie samochodu: mniej więcej 2. Widać wyraźnie, iż samochód przyspieszał znacznie (8 krotnie) szybciej aniżeli pociąg.

Definicja - Ruch jednostajnie przyspieszony, prostoliniowy

Ruch, którego torem bywa prosta prosta, szybkość rośnie, a przyrost prędkości bywa ten sam w każdej sekundzie ruchu.

tor bywa linią prostą,
prędkość rośnie o stałą cena przyspieszenia w każdej sekundzie ruchu.

Przyspieszenie

Przy opisie ruchu podajemy przyspieszenie - aczkolwiek nie wpływa ono bezpośrednio na drgnienie - określa, jeśli zmienia się prędkość. Jest wektorem, podobnie jeśli prędkość. Zawiera więc dodatkowe informacje - kierunek, zwrot. Jeśli zgadzają się z wektorem prędkości, wówczas szybkość rośnie.

Jednak zwrot przyspieszenia może istnieć inny, gdy bywa nieprzychylny aniżeli szybkość - zmniejsza ją, czyli hamuje. Żeby rozróżnić ten ruch, nazywamy go ruchem opóźnionym.

Wzór - postać wektorowa i wykres.

przyspieszenie: $\vec a =\frac{_{\Delta} \vec v}{t} \qquad \left [\frac{m}{s^2} \right ]$

Przyspieszenie bywa stałe (a = const).

Prędkość
Jeżeli organizm poruszało się poprzez pewien termin z przyspieszeniem a, znajdziemy tego prędkość. Skorzystamy ze wzoru na przyspieszenie i przekształcimy go na wzór opisujący szybkość (zakładamy, iż przed ruchem szybkość była 0):

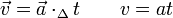
prędkość: $\vec v =\vec a \cdot _{\Delta}t \qquad v = at$

Fragment wykresu prędkości od czasu, v rośnie proporcjonalnie do t.

Droga
W ruchu pojawiło się przyspieszenie, a szybkość stale rośnie - jeśli to wpływa na przebytą drogę? Wyobraźmy sobie - w pierwszej sekundzie szybkość wynosi 1m/s. Jednak po 5 sekundach może wzrosnąć do 10m/s. Oznacza to, iż po pewnym czasie (gdy szybkość wzrośnie) poprzez 1 sekundę pokonamy więcej drogi aniżeli poprzednio (przy małej prędkości). Musimy zapomnieć o wzorze z ruchu jednostajnego, nie potrafi on opisać tego ruchu. Okazuje się, iż trasa rośnie kwadratowo względem czasu, wzór:

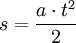
droga: $s= \frac{a\cdot t^2}{2}$

Przy odrobinie wysiłku, możemy ten wzór obliczyć, robią to jednocześcnie studenci, choć zrezygnujemy z tego.

Czasami opisujemy ruch, w którym organizm zaczyna z pewną prędkością początkową, nadobowiązkowo znajdując się w pewnej odległości od miejsca, od którego mierzymy drogę. Dane te możemy uwzględnić we wzorze, tzn. zsumujemy drogę początkową, namowa prędkości początkowej i dotychczasowy wzór na drogę:

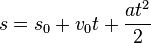
$s = s_0+v_0t+\frac{a t^2}{2}$

przebyta trasa = trasa początk. + namowa prędkości początk. + trasa przebyta 'z przyspieszenia'

Droga rośnie 'kwadratowo' względem czasu.

Ruch opóźniony

Mówimy, iż drgnienie bywa opóźniony, gdy przyspieszenie skierowane bywa przeciwnie aniżeli prędkość. Prędkość początkowa v₀ maleje, bywa zmniejszana z powodu przyspieszenia. Wektor bywa przeciwnie skierowany, a wiemy, iż dodanie przeciwnego wektora wiąże się z postawieniem przy nim minusa:

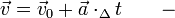$\vec v = \vec v_0 + \vec a \cdot _{\Delta}t \qquad -$ w tutejszym lokalizacji występuje dodawanie przeciwnych wektorów $\vec v_0 \;\; \mbox{i} \;\; \vec a$

bez wektorów:

$v = v_0 + (-a)\cdot t \qquad - \,\vec a$ bywa przeciwne do ruchu, co skutkuje minusem

podobne rozumowanie do wzoru na drogę:

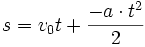
$s= v_0t + \frac{-a\cdot t^2}{2}$

Nie stworzyliśmy nowych wzorów, a jedynie wprowadziliśmy poprawkę do poprzednich (w ruchu opóźnionym przyspieszenie bywa przeciwnie skierowane, dlatego wstawiamy minus; nadobowiązkowo zawsze występuje szybkość początkowa).

Ciało osiąga szybkość równą zero (zatrzymuje się) po czasie t_k, tzn. w chwili końca ruchu.

Czas zatrzymania się
Ciało z przyspieszeniem przeciwnym do kierunku ruchu zaczyna zwalniać, do momentu zatrzymania. Jeśli interesuje nas, gdy organizm się zatrzyma, wystarczy iż przekształcimy wzór na szybkość (uwzględniając, iż w takiej chwili zatrzymane organizm posiada szybkość v=0):

$v=0\;$

$\vec v=\vec v_0 + \vec a t$

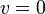
wektor a posiada nieprzychylny zwrot, zmienia się znak:

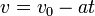
$v = v_0 - at\;$

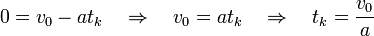
$0 = v_0-a t_k \quad \Rightarrow \quad v_0 = a t_k \quad \Rightarrow \quad t_k = \frac{v_0}{a}$

Dodatkowe wzory

Jeśli ze wzoru

$v = v_{0} + at\,$

wyznaczymy t i podstawimy do czasu w równaniu

$s = v_0t+\frac{a t^2}{2}$ ,

to po przekształceniach otrzymamy tak zwane równanie bez czasu:

$v^{2} - v_{0}^{2} = 2as$

Wzór ten znajduje zastosowanie w obu ruchach - przyspieszonym i opóźnionym. W ruchu opóźnionym szybkość końcowa bywa mniejsza od początkowej, co sprawi, iż lewa strona równania będzie ujemna (tym samym jednocześcnie prawa), co oznacza, iż z prawej strony ujemne będzie przyspieszenie, a więc drgnienie będzie opóźniony.

Wzór ten możemy wykorzystać do wyprowadzenia kolejnego. Wyznaczmy więc s:

$s\, =\frac {v^{2} - v_{0}^{2}}{2a}$

Jest on prawdziwy do ruchu przyspieszonego z prędkością początkową. W ruchu przyspieszonym bez prędkości początkowej (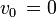 $v_{0}\,=0$ ) wzór przyjmuje postać:

$s\, =\frac {v^{2}}{2a}$

Podobnie w ruchu opóźnionym, w którym szybkość końcowa równa bywa zero, podstawienie zera uprości wzór do jednej prędkości (jak powyżej).

Zadania

Zad. 1 (przyspieszenie) Pocisk wystrzelony z karabinu porusza się z przyspieszeniem 500 km/s² i prędkością początkową 800m/s. Oblicz, jaką przebędzie odległość w ciągu 0,1 sekundy.

dane

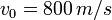
$v_0 = 800 \,m/s \,$

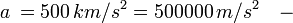$a \,= 500 \,km/s^2 = 500 000 \,m/s^2 \quad-$ zamiana na jednostki podstawowe

$t \,= 0,1 \,s$

rozwiązanie

Odległość policzymy ze wzoru na drogę; pocisk miał aczkolwiek szybkość początkową, którą również uwzględniamy:

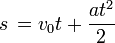
$s \,= v_0t + \frac{at^2}{2}$

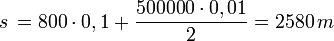
$s \,= 800 \cdot 0,1 + \frac{500 000 \cdot 0,01}{2} = 2580 \,m$

Wykonajmy nadobowiązkowo obliczenia na jednostkach, w celu sprawdzenia:

szkic: $\left [\tfrac{m}{s} \right ] \cdot [s] + \frac{\left [\tfrac{m}{s^2} \cdot s^2 \right ]}{[-]} \;=\; [m] + [m] = [m]$

Czytany 15151 razy Ostatnio zmieniany wtorek, 30 listopada 2010 20:53

Opublikowano w Kinematyka

Z etykietą

Podziel się tym z innymi

dr inż. Paweł Troka

Owner & CEO
E-Mail: ptroka@fizyka.dk
PTroka on Google+

Strona: fizyka.dk

Najnowsze od dr inż. Paweł Troka

Artykuły powiązane

Więcej w tej kategorii: « Podstawy dotyczące ruchu ciał Ruch jednostajny po okręgu »

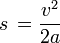
Komentarze

0 #3 Paula 2011-10-12 21:17

Dziękuję bardzo za rozwiązanie i podpowiedź:)
Już teraz będę wiedziała gdzie co przesłać.
A, i jeszcze raz dziękuję za Waszą stronę - jesteście fantastyczni jeszcze trochę, a zacznę lubić fizykę (jak na razie staram się podchodzić do niej pozytywnie - zgodnie z Waszym poradnikiem:))

Cytować | Zgłoś administratorowi

+2 #2 mgr inż. Vojtech Mańkowski 2011-10-12 21:09

Odpowiedź na pytanie Pauli.

1.Równość prędkości.
Przyjmując, że na wykresie XY, y będzie szybkością a x czasem, to rysujesz dwie proste:
y=2x, odpowiednik v=at
y=10, stała prędkość kolarza
Punkt przecięcia (t=x=5) to zrównanie prędkości.

2.Samochód dogania kolarza.
Tym razem y to będzie odleglosc, a x znowu czas t.
y=0.5*2x^2
Dla samochodu (słynne s=1/2at^2) krzywa jest parabolą.
y=200 + 10x
Dla kolarza to będzie prosta przesunięta do góry o 200.
------
Tak na przyszłość, pytania dotyczące zadań prosimy umieszczać na FORUM, bądź też przesyłać na nasze maile, które są widoczne w dziale REDAKCJA

Cytować | Zgłoś administratorowi

0 #1 Paula 2011-10-10 21:15

A co jeśli mam zadanie:

Samochód rusza się z a= 2 m/s2. Przed nim, w odległości 200m jechał kolarz ruchem jednostajnym z V = 10 m/s. Znajdź graficznie czas po którym prędkości będą równe oraz czas po którym ciało dogoni kolarza.

BŁAGAM O POMOC!

Cytować | Zgłoś administratorowi

Odśwież komentarze
Kanał RSS z komentarzami do tego postu.

Dodaj komentarz

powrót na górę

Menu Główne

Dla miłośników

Edukacja

Poradniki

Pomoc w nauce

| Jeżeli w zasobach naszego serwisu nie znalazłeś tego czego szukałeś prosimy napisz do nas na e-mail: sugestie@fizyka.dk a my uzupełnimy te braki |

Korepetycje

Polecane książki

Ruch przyśpieszony

Ruch jednostajnie przyśpieszony

Przyspieszenie

Ruch opóźniony

Dodatkowe wzory

Zadania

dr inż. Paweł Troka

Najnowsze od dr inż. Paweł Troka

Artykuły powiązane

Komentarze

Dodaj komentarz

Online:

Logowanie

Tagi

Menu Główne

Dla miłośników

Edukacja

Poradniki

Pomoc w nauce

Ostatnio dodane

Ostatnio modyfikowane

Ostatnio skomentowane

Najlepiej oceniane

Najczęściej czytane

Najwięcej komentarzy

Archiwum