Ruch jednostajny po okręgu
Ciało porusza się ruchem jednostajnym i torem tego ruchu bywa okrąg.
| Definicja - Ruch jednostajny po okręgu |
| Ruch jednostajny po okręgu bywa przypadkiem ruchu krzywoliniowego, którego cena prędkości nie ulega zmianie. W ruchu występuje moc dośrodkowa, która powoduje powstanie przyspieszenia dośrodkowego(normalnego), jakie powoduje zmianę kierunku wektora prędkości. |
| Przykład - Ruchy po okręgu |
Najprostsze przykłady tego ruchu spotykane w życiu codziennym:
|
Jedną z cech tego ruchu bywa wielkość zwana okresem T. Jest to czas, w ciągu którego organizm pokonuje całą długość toru - czyli obwód koła. Oznacza to, iż po czasie T organizm wraca do 'punktu wyjścia'.
Czas jednego obrotu, czyli okres, możemy zamienić na inną wielkość - częstotliwość (częstość). Jest to liczba obrotów wykonanych w ciągu jednostki czasu. Przykładowo, wał w silniku może wykonywać 3000 obrotów na minutę.
- częstotliwość
![\nu\,=\frac{1}{T} \;\; [\mbox{Hz}] = \left [\frac{1}{s}\right ]\qquad -](http://upload.wikimedia.org/math/d/d/d/ddd881c07e9aac57a3fcf12b5eb897ee.png) zależność pomiędzy częstotliwością i okresem, jednostka Herc.
zależność pomiędzy częstotliwością i okresem, jednostka Herc.
Prędkość takiego ciała obliczamy jeśli w ruchu jednostajnym. Wiemy, iż drogę s równą obwodowi koła pokonuje w czasie równym okresowi, podstawmy te dane do wzoru.
- wartość prędkości liniowej (szybkość)
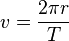
- wektor
 bywa styczny do okręgu.
bywa styczny do okręgu.
Prędkość liniowa bywa zawsze skierowana stycznie do okręgu - co oznacza, iż zwrot prędkości podczas ruchu cały termin się zmienia, cały termin bywa styczne do okręgu, poprzez co organizm 'zakreśla' okrąg. Jednak co wpływa na to, iż szybkość liniowa bywa cały termin styczna do okręgu ruchu? Przyczyną tego bywa przyspieszenie dośrodkowe, jakie omówione zostanie dalej.
Szybkość możemy uzewnętrznić jednocześcnie w odmienny sposób, przy pomocy kąta, jaki zakreśliło organizm poruszając się po okręgu w danym czasie. Jeśli punkt początkowy i docelowy ruchu połączymy liniami z środkiem okręgu, to linie te utworzą właśnie zakreślony poprzez organizm kąt  .
.
- szybkość kątowa
![\omega \,= \frac{\alpha}{t}\qquad \left [\frac{rad}{s} \right ] \mbox{lub} \left [\frac{1}{s} \right ]](http://upload.wikimedia.org/math/d/b/e/dbea09ac019069d7307dfa25c0f2bd9b.png)
Przykład
Satelita znajduje się w odległości 40000km od środka Ziemi, zawsze nad takim samym punktem Ziemi (porusza się 'równo' z planetą). Opiszmy ten ruch:
- 1. okres
 w takim czasie satelita wykona pełny obrót wokół Ziemi
w takim czasie satelita wykona pełny obrót wokół Ziemi
- 2. częstotliwość
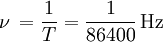
- Przebytą drogę obliczymy licząc obwód okręgu:
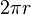 , dokąd r to promień okręgu. Promieniem bywa odległość satelity od środkowego punktu (środka Ziemi), drobiazgowo ten wymiar mamy podany w zadaniu.
, dokąd r to promień okręgu. Promieniem bywa odległość satelity od środkowego punktu (środka Ziemi), drobiazgowo ten wymiar mamy podany w zadaniu.
- 3. szybkość liniowa (v=s/t):
![v\,= \frac{2\pi r}{T} = \frac{2 \pi \cdot 40 000 000 }{86400}\, \left [\frac{m}{s} \right ] \qquad -](http://upload.wikimedia.org/math/3/7/2/372536af3a05ebf80a8dc22d4f821708.png) ze zmianą jednostek
ze zmianą jednostek
- Aby policzyć szybkość kątową, skorzystajmy z faktu, iż satelita przebędzie całą drogę w czasie równym okresowi T (wynika to z definicji okresu). Zakreśli przy takim kąt pełny, czyli 360o =
 .
.
- 4. szybkość kątowa
![\omega \,= \frac{\alpha}{t} = \frac{2\pi}{86400} \quad \left [\frac{rad}{s} \right ]](http://upload.wikimedia.org/math/6/0/c/60cabfe2038a77d1b976a1442ffadc00.png)
Warto wiedzieć, jeśli możemy obliczyć kąt, jaki zakreśla ciało. Jest to stosunek łuku s (łuk to droga, którą przebywa ciało) do promienia r:
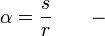 s to zakreślony łuk
s to zakreślony łuk
Dzięki temu możemy zapisać zależność pomiędzy prędkością kątową a prędkością liniową
- mając
 otrzymujemy zależność
otrzymujemy zależność 
- szybkość kątowa a liniowa:
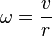
Przyspieszenie dośrodkowe
W ruchu po okręgu występuje siła dośrodkowa (więcej o siłach w dalszych częściach podręcznika), która nadaje ciału przyspieszenie dośrodkowe. Przyspieszenie to zmienia kierunek wektora prędkości, przy czym nie zmienia tego wartości.
Siłę tę możemy policzyć,  , gdzie: m - masa ciała, v - cena prędkości liniowej (szybkość), r - promień okręgu (toru ruchu). Siła ta bywa skierowana do środka okręgu.
, gdzie: m - masa ciała, v - cena prędkości liniowej (szybkość), r - promień okręgu (toru ruchu). Siła ta bywa skierowana do środka okręgu.
Przyspieszenie dośrodkowe ar bywa skutkiem działania siły dośrodkowej. Można je policzyć ze wzoru zawierającym szybkość liniową i promień okręgu:
Skierowane bywa jednocześcnie do środka okręgu. Jak już zostało wspomniane, przyspieszenie to powoduje zmianę kierunku wektora prędkości, tak by był cały termin styczny do toru ruchu, skutkiem czego organizm porusza się właśnie ruchem po okręgu. Nie zmienia wartości prędkości ciała, stąd drgnienie bywa jednostajny.
Podsumowanie
- ciało porusza się ruchem jednostajnym krzywoliniowym po okręgu o promieniu r
- okres T to odwrotność częstotliwości
- wartość prędkości liniowej v (jak w ruchu jednostajnym) bywa równa drodze podzielonej poprzez czas. W szczególnym przypadku drogą może istnieć obwód koła 2?r, wówczas termin bywa gładki okresowi (
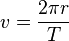 )
) - ciało po pewnym czasie zakreśla kąt
 , jaki możemy policzyć poprzez podzielenie przebytego łuku poprzez promień okręgu (
, jaki możemy policzyć poprzez podzielenie przebytego łuku poprzez promień okręgu (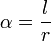 )
) - szybkość kątowa
 bywa równa zakreślonemu kątowi podzielonemu poprzez czas, w jakim został zakreślony. W szczególności, kąt pełny zakreślony bywa w czasie równym okresowi (
bywa równa zakreślonemu kątowi podzielonemu poprzez czas, w jakim został zakreślony. W szczególności, kąt pełny zakreślony bywa w czasie równym okresowi (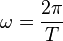 )
) - przyspieszenie dośrodkowe ar równe bywa kwadratowi wartości prędkości podzielonemu poprzez promień; po podstawieniach możemy uzyskać inne wzory (
 )
) - wektor przyspieszenia (
 ) skierowany bywa prostopadle do toru ruchu (okręgu), czyli do środka okręgu; wektor prędkości (
) skierowany bywa prostopadle do toru ruchu (okręgu), czyli do środka okręgu; wektor prędkości ( ) skierowany bywa stycznie do okręgu
) skierowany bywa stycznie do okręgu






























Komentarze
pl.wikibooks.org/wiki/Fizyka_dla_liceum/Ruch_po_okr%C4%99gu
Kanał RSS z komentarzami do tego postu.