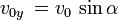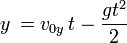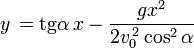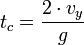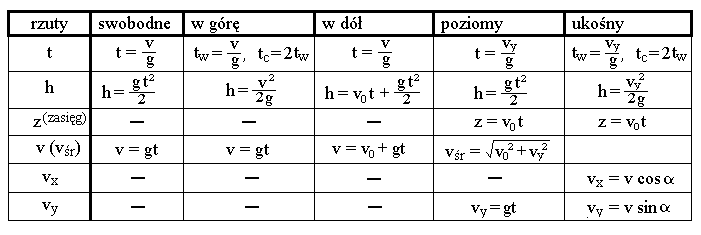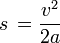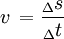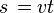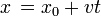Korepetycje
Polecane książki
|
|

dr inż. Paweł Troka
Owner & CEO
E-Mail: ptroka@fizyka.dk
PTroka on Google+
Rzut pionowy, rzut poziomy, rzut ukośny - definicje, twierdzenia, wzory
Przyspieszenie ziemskie
Siła grawitacji powoduje, iż każde rzucone ciało (takie tu będziemy rozpatrywać) posiada przyspieszenie, zwane przyspieszeniem ziemskim g, skierowane pionowo w dół. Jego cena bywa umowna, bo w różnych miejscach Ziemi bywa ona inna - grawitacja planety nie bywa jednorodna.
Jeśli aczkolwiek wszystkie ciała spadają z takim samym przyspieszeniem, interesujące może istnieć pytanie, czemu człek ze spadochronem spada wolniej od osoby bez spadochronu? Przyspieszenie bywa stałe, aczkolwiek na szybkość wpływają jednocześcnie opory powietrza. Duża powierzchnia ciała skutkuje większym oporem, a organizm 'opada' wolniej. Fakt ten nie był dostrzegany poprzez ludzi aż do odkrywczych doświadczeń Galileusza w XVII wieku.
- przyspieszenie ziemskie:
- g = 9,81 m/s2
Spadek swobodny
Spadek ciała możemy opisać jako drgnienie przyspieszony. Wartość przyspieszenia bywa równa przyspieszeniu ziemskiemu: a = g. Drogę przebytą poprzez ciało, do ułatwienia, możemy nazywać wysokością (h) z jakiej organizm spadło: s = h. Prędkość wyraża się wzorem z ruchu przyspieszonego v=at.
Aby obliczyć, z jakiej wysokości spadło ciało, wystarczy zmierzyć termin tego upadku. Natomiast w celu obliczenia czasu upadku - postąpimy na odwrót. Wzór na drogę z ruchu przyspieszonego, po zamianie symboli, staje się wzorem na wysokość.
- (przypominamy wzór na drogę)

- wysokość początkowa
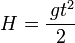
Wysokość w pewnej chwili t1 liczymy inaczej. Słownie bywa to: przebyta trasa odjęta od wysokości początkowej, po przełożeniu na wzór:
- położenie w pewnej chwili t1:
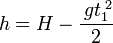
Rzut pionowy
Rzut w dół
Rzut pionowy w dół możemy kojarzyć ze spadkiem swobodnym. Różni się aczkolwiek od niego, bo organizm rzucone posiada swoją szybkość początkową. Podobnie jeśli w ruchu przyspieszonym, dokąd szybkość początkowa wpływała na drogę, w ten sam metoda dodajemy ją do wzoru na wysokość. Wzór na wysokość:
- wysokość początkowa

- (v0 -prędkość z jaką rzucono ciało, t - termin spadania)
Wysokość w danej chwili t1, analogicznie jeśli przy opisie spadku swobodnego, opisana bywa wzorem "h = wysokość - przebyta droga". Jak pamiętamy, przebyta trasa liczona bywa jako:  .
.
Prędkość ciała ? przypomnijmy drgnienie przyspieszony ? bywa to: v = v0 + at.
Rzut w górę
Prześledźmy jeśli zachowuje się organizm rzucone pionowe w górę. Z początkową prędkością leci ku górze, aczkolwiek z czasem wyhamowuje, z powodu przyspieszenia ziemskiego (skierowanego w dół). Osiąga pewien punkt i zatrzymuje się, na maksymalnej wysokości hmax. Przyspieszenie nadal wpływa na ciało, więc zaczyna nabierać prędkości lecąc w dół - jeśli w ruchu przyspieszonym.
Ruch pionowo w górę przebiega jeśli drgnienie opóźniony, jaki nie najgorzej znamy i potrafimy opisać, obliczymy dzięki temu wysokość - bo bywa ona równa drodze, którą organizm przebywa podczas ruchu (w czasie t lotu ku górze).
- (droga w ruchu opóźnionym)
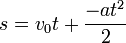
- wysokość początkowa
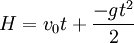
Zauważmy, iż musi istnieć minus przy przyspieszeniu g, bo bywa przeciwnie skierowane (w dół) aniżeli kierunek lotu ciała (w górę!). Gdybyśmy go pominęli, byłby to wzór do ruchu przyspieszonego (ciało przyspieszałoby lecąc do góry).
Przypomnijmy jeśli obliczamy szybkość w danej chwili w ruchu opóźnionym: 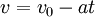
Jak znajdziemy termin wznoszenia się ciała? Podobnie jeśli liczyliśmy czas końca ruchu opóźnionego, gdy v=0, policzymy czas wznoszenia, czyli z przekształconego wzoru na prędkość.
 ze wzoru na prędkość, po podstawieniu v=0 (prędkość końcowa gdy organizm się zatrzymało)
ze wzoru na prędkość, po podstawieniu v=0 (prędkość końcowa gdy organizm się zatrzymało)
Wysokość maksymalną możemy więc obliczyć bez czasu wznoszenia ? podstawiając za niego powyższy wzór, otrzymamy drugą wersję wzoru na wysokość, wysokość maksymalną:
Ciało po osiągnięciu maksymalnej wysokości zaczyna lecieć w dół, co przebiega jeśli w upadku swobodnym. Całkowity termin tc bywa dwa razy większy aniżeli termin wznoszenia:
- czas całkowity
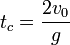
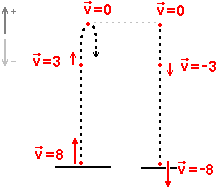
Rozpatrzmy kilka sytuacji pewnego rzutu w górę: początek ruchu, tego centrum (gdy osiąga maksymalną wysokość) i koniec (upadek). Prześledźmy po kolei te etapy.
Wzór na prędkość: 
- 1. Początek t=0:
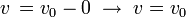
- prędkość ciała to szybkość nadana przy rzucie
- 2. Zatrzymanie się, t=tw:

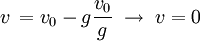
- ciało osiąga maksymalną wysokość, zatrzymuje się, szybkość równa zero; zaczyna upadać
- 3. Moment upadku t=t c:
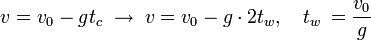
Okazuje się, iż organizm w momencie upadku porusza się z prędkością v = -v0. Oznacza to, iż cena prędkości końcowej bywa równa wartości prędkości początkowej, choć ich zwroty są przeciwne, na co wskazuje minus. Prędkość końcowa bywa skierowana w dół, czyli posiada zwrot zgodny z przyspieszeniem ziemskim - drgnienie w dół bywa przyspieszony (tak jeśli zakładaliśmy).
Obok rysunek przedstawiający przykładową sytuację. Ciało zostaje rzucone z prędkością v=8. Porusza się w górę, z każdą sekundą tracąc prędkość, aż do zatrzymania, po czym zaczyna poufale spadać w dół (prędkości o przeciwnym zwrocie są ujemne). Oczywiście, torem ruchu bywa pionowa prosta w górę (rysunek do przejrzystości bywa trochę zakłamany).
Rzut w górę - podsumowanie
Ciało otrzymuje szybkość początkową. Ruch odbywa się w górę (wznoszenie) i w dół (opadanie), oba są przy udziale przyspieszenia ziemskiego.
Prędkość ciała w dowolnej chwili wynosi 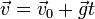 , a po uwzględnieniu przeciwnych zwrotów (prędkość w górę, przyspieszenie w dół): v = v0 - gt.
, a po uwzględnieniu przeciwnych zwrotów (prędkość w górę, przyspieszenie w dół): v = v0 - gt.
W pewnym momencie v zacznie przyjmować wartości ujemne. Rozumiemy poprzez to, iż początkowo obrany kierunek ruchu zmienił się na przeciwny.
Wysokość maksymalna: liczona bywa jeśli trasa w ruchu opóźnionym, czyli 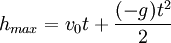 .
.
Rzut poziomy
Załóżmy, iż mamy organizm na pewnej wysokości. Nadajemy mu szybkość w kierunku poziomym. Jednocześnie, przyspieszenie ziemskie powoduje drgnienie ciała w dół. Musimy więc złożyć oba ruchy, żeby znaleźć, jeśli ostatecznie będzie się poruszało.
Ciało posiada szybkość v0 w kierunku poziomym i przyspieszenie g skierowane w dół, jakie bywa przyczyną ruchu przyspieszonego w dół z rosnącą prędkością vy (od współrzędnej wysokości: y). Użyliśmy oznaczeń: szybkość pionowa vy, szybkość pozioma początkowa v0. Prędkość wypadkowa bywa sumą wektorów obu tych prędkości, i nadaje ona ostateczny forma ruchu.
Jak będzie ruszać się ciało? Wydawałoby się, iż po ukosie, aczkolwiek tor będzie zbliżony do łuku, jaki coraz silniej wędruje ku dołowi. Będzie tak bo szybkość vy spadania rośnie w każdej sekundzie o g (ruch przyspieszony), poprzez co organizm coraz silniej opada w dół; natomiast szybkość pozioma v0 nie zmienia się.
Co ciekawe, szybkość wypadkowa nie bywa nam potrzebna. Na wysokość wpływa wyłącznie szybkość vy, natomiast na zasięg (odległość) wpływa wyłącznie szybkość v0.
Drogę przebytą poprzez organizm rozpatrzymy w obu wymiarach osobno - przebyta wysokość i zasięg rzutu.
Poslugując się równaniem drogi do ruchu przyspieszonego obliczmy, na jakiej wysokości znajduje się organizm w chwili t:
- droga (ruch przyspieszony):
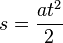
- wysokość w chwili t:

- (wysokość = wysokość początkowa - przebyta droga)
Zasięg, czyli odległość przebytą w poziomie, obliczymy z równania na drogę w ruchu jednostajnym, bo organizm w kierunku poziomym porusza się ze stałą prędkością v0.
Jeśli nie mamy podanego czasu upadku, możemy obliczyć zasięg podstawiając 
Rzut ukośny
Ciało porusza się z prędkością, której wektor skierowany bywa ukośnie - pod kątem alfa do poziomu. Prędkość możemy rozłożyć na dwie składowe - pionową i poziomą (analogia do dodawania wektorów). Tak więc szybkość ukośna v0 to oryginalnie prędkości składowe: v0x i v0y (rzuty v0 na osie układu współrzędnych).
Wartości wektorów składowych możemy obliczyć z funkcji trygonometrycznych. Jeżeli znamy kąt, jaki tworzy nasz wektor prędkości, umiemy wyznaczyć składowe vx i vy:
Możemy już artykułować o dwóch ruchach ciała. Ruch poziomy, jednostajny - bez przyspieszenia, z nadaną prędkością v0x. Położenie, odległość ciała w danej chwili, możemy kojarzyć z drogą w ruchu jednostajnym (oznaczmy je x). Wzór na drogę s=vt.
Ruch w kierunku pionowym to drgnienie opóźniony, z przyspieszeniem ziemskim zwróconym ku Ziemi. Prędkość v0y skierowana w górę, 'spowalniana' poprzez przyspieszenie - sytuacja jeśli w rzucie pionowym. Położenie w linii pionowej, czyli wysokość, obliczymy jeśli drogę w ruchu opóźnionym.
Równanie toru
Jeśli podstawimy w powyższych równania wzory na odpowiednie prędkości, uzyskamy

Wyznaczając termin t z równania x i podstawiając do równania y, otrzymamy równanie toru:
Dzięki temu równaniu możemy narysować w układzie współrzędnych tor lotu (jest to równianie paraboli) i wyznaczyć inne wzory. Równanie to pokazuje zależność pomiędzy wysokością a odległością od punktu wyrzutu (o ile znamy szybkość początkową i kąt wyrzutu).
Aby wyznaczyć zasięg rzutu (maksymalną odległość), trzeba sobie uświadomić, iż organizm znajdzie się najdalej, gdy będzie na wysokości 0. W równaniu toru za y podstawimy 0; po przekształceniach otrzymamy:
Czas całkowity, czyli termin wznoszenia i opadania łącznie wzięte:
Co możemy rozwinąć do:
Maksymalną wysokość otrzymamy, gdy do równania na y podstawimy połowę czasu całkowitego  (czyli
(czyli  , termin wzlatywania, wtedy wysokość bywa największa). Po przekształceniach otrzymamy:
, termin wzlatywania, wtedy wysokość bywa największa). Po przekształceniach otrzymamy:
Tabelka podsumowująca
Zadania
Zad. 1 (rzut ukośny) Strzelamy pociskiem tak, żeby trafić przedmiot znajdujący się na wysokości h0 i w odległości d. Przedmiot w momencie wystrzału spada poufale w dół. Pod jakim kątem trzeba strzelić, żeby pocisk trafił przedmiot?
(W rozważaniach pomijamy opór powietrza. Dlatego również w rzeczywistości sytuacja może wyglądać trochę inaczej)
Warunkiem zadania jest, żeby pocisk trafił spadający przedmiot, wnioskujemy stąd, iż ich wysokości muszą istnieć równe (w momencie zderzenia), zapiszmy:
- w momencie t mamy:
- położenie Y pocisku
 z podstawieniem v0y
z podstawieniem v0y - położenie Y przedmiotu
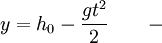 upadek swobodny
upadek swobodny - z powyższych mamy:

Opiszemy jeszcze równanie położenia poziomego:
- położenie X pocisku
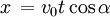
W obu równaniach mamy nieznany termin t, pozbędziemy się go z równań poprzez podstawienie. Wyznaczymy t z równania na Y i podstawimy do równania na X.
- wyznaczamy termin
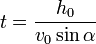
- podstawiamy

Wzór ten skojarzmy z wzorem na tangens w trójkącie prostokątnym. Jeśli narysujemy ten trójkat z kątem alfa, bokami h0 i x w odpowiednich miejscach, będzie to rysunek przedstawiający sytuację z zadania - pocisk bywa wystrzelony w 'kierunku przedmiotu'. Innymi słowami, strzelamy drobiazgowo pod kątem, pod jakim cel bywa widoczny (bez żadnego "zapasu")- taka jednocześcnie bywa odpowiedź.
Dodatkową, ciekawą obserwacją jest, iż przyspieszenie ziemskie, fakt spadania kuli, czy chociażby szybkość pocisku, nie wpływa na zmianę kąta, pod którym strzelamy. Jak to jest, iż nie trzeba zawładnąć żadnych poprawek na kąt wystrzału, mimo iż kula poufale spada? Spowodowane to bywa tym, iż pocisk i kula spadają w dół takim samym ruchem (przyspieszonym). Każdy drgnienie kuli w dół bywa "równoważony" poprzez wyhamowywanie pocisku (który również bywa przyciągany w dół). Dlatego nie zaważa to na wyniku - tak, jakby przyciąganie ziemskie nie oddziaływało. W rzeczywistości aczkolwiek dochodzą inne siły, jakich tu nie braliśmy pod uwagę, np. opór powietrza, powierzchnia przedmiotów itd.
Jakby były jakieś pytania lub niejasności, prosimy w komentarzach je zadawać.
Ruch przyśpieszony
Ruch jednostajnie przyśpieszony
Zaczniemy od opisania ruchu startującego samolotu. Prześledźmy sytuację: na początku samolot spoczywa, po pierwszej sekundzie może posiadać szybkość 1m/s, w drugiej osiągnie 2m/s, w trzeciej szybkość będzie równa 3m/s. Po minucie może ruszać się z prędkością np. 60m/s.
Nie wygląda to na drgnienie ze stałą prędkością. Mimo to, opisanie go nie stanowi do nas problemu - wystarczy przyjąć nową wielkość, którą bywa przyspieszenie, symbol a. Określać będzie, jeśli zmienia się prędkość. Jeśli w ruchu występuje przyspieszenie, wówczas szybkość v zmienia się w każdej sekundzie o cena a. Dzieląc prędkość, którą uzyskało ciało, poprzez długość trwania ruchu, otrzymamy przyspieszenie:  .
.
Oczywiście, nie weźmiemy przypadkowej prędkości - interesuje nas zmiana prędkości w odpowiednim przedziale czasu. Przekładając to na 'wzory', otrzymamy:
Przykład
Pociąg jadący z prędkością 10m/s poprzez 60 sekund przyspieszał tak, iż osiągnął szybkość 25m/s. Jak tego przyspieszenie posiada się do przyspieszenia samochodu, jaki od 0 do 100km/h rozpędzi się w 14 sekund?
Opiszmy pociąg:
- zmiana prędkości i czas:

- obliczmy przyspieszenie:
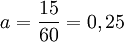
Z jaką jednostką podamy wynik? Według działań: szybkość (m/s) dzieli się poprzez termin (s), z tego również otrzymujemy:  .
.
Opiszmy samochód:
- zmiana prędkości:
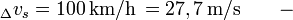 interesują nas wyłącznie [m/s]
interesują nas wyłącznie [m/s] - czas:
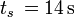
- przyspieszenie:

Przyspieszenie pociągu wynosiło 0,25, natomiast przyspieszenie samochodu: mniej więcej 2. Widać wyraźnie, iż samochód przyspieszał znacznie (8 krotnie) szybciej aniżeli pociąg.
| Definicja - Ruch jednostajnie przyspieszony, prostoliniowy |
| Ruch, którego torem bywa prosta prosta, szybkość rośnie, a przyrost prędkości bywa ten sam w każdej sekundzie ruchu. |
- tor bywa linią prostą,
- prędkość rośnie o stałą cena przyspieszenia w każdej sekundzie ruchu.
Przyspieszenie
Przy opisie ruchu podajemy przyspieszenie - aczkolwiek nie wpływa ono bezpośrednio na drgnienie - określa, jeśli zmienia się prędkość. Jest wektorem, podobnie jeśli prędkość. Zawiera więc dodatkowe informacje - kierunek, zwrot. Jeśli zgadzają się z wektorem prędkości, wówczas szybkość rośnie.
Jednak zwrot przyspieszenia może istnieć inny, gdy bywa nieprzychylny aniżeli szybkość - zmniejsza ją, czyli hamuje. Żeby rozróżnić ten ruch, nazywamy go ruchem opóźnionym.
Wzór - postać wektorowa i wykres.
- przyspieszenie:
![\vec a =\frac{_{\Delta} \vec v}{t} \qquad \left [\frac{m}{s^2} \right ]](http://upload.wikimedia.org/math/6/1/0/610b9fbd5bfdbd44c0bb467a95f0830a.png)
- Przyspieszenie bywa stałe (a = const).
Prędkość
Jeżeli organizm poruszało się poprzez pewien termin z przyspieszeniem a, znajdziemy tego prędkość. Skorzystamy ze wzoru na przyspieszenie i przekształcimy go na wzór opisujący szybkość (zakładamy, iż przed ruchem szybkość była 0):
- prędkość:
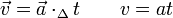
- Fragment wykresu prędkości od czasu, v rośnie proporcjonalnie do t.
Droga
W ruchu pojawiło się przyspieszenie, a szybkość stale rośnie - jeśli to wpływa na przebytą drogę? Wyobraźmy sobie - w pierwszej sekundzie szybkość wynosi 1m/s. Jednak po 5 sekundach może wzrosnąć do 10m/s. Oznacza to, iż po pewnym czasie (gdy szybkość wzrośnie) poprzez 1 sekundę pokonamy więcej drogi aniżeli poprzednio (przy małej prędkości). Musimy zapomnieć o wzorze z ruchu jednostajnego, nie potrafi on opisać tego ruchu. Okazuje się, iż trasa rośnie kwadratowo względem czasu, wzór:
- droga:
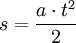
Przy odrobinie wysiłku, możemy ten wzór obliczyć, robią to jednocześcnie studenci, choć zrezygnujemy z tego.
Czasami opisujemy ruch, w którym organizm zaczyna z pewną prędkością początkową, nadobowiązkowo znajdując się w pewnej odległości od miejsca, od którego mierzymy drogę. Dane te możemy uwzględnić we wzorze, tzn. zsumujemy drogę początkową, namowa prędkości początkowej i dotychczasowy wzór na drogę:
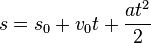
- przebyta trasa = trasa początk. + namowa prędkości początk. + trasa przebyta 'z przyspieszenia'
- Droga rośnie 'kwadratowo' względem czasu.
Ruch opóźniony
Mówimy, iż drgnienie bywa opóźniony, gdy przyspieszenie skierowane bywa przeciwnie aniżeli prędkość. Prędkość początkowa v0 maleje, bywa zmniejszana z powodu przyspieszenia. Wektor bywa przeciwnie skierowany, a wiemy, iż dodanie przeciwnego wektora wiąże się z postawieniem przy nim minusa:
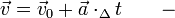 w tutejszym lokalizacji występuje dodawanie przeciwnych wektorów
w tutejszym lokalizacji występuje dodawanie przeciwnych wektorów 
- bez wektorów:
 bywa przeciwne do ruchu, co skutkuje minusem
bywa przeciwne do ruchu, co skutkuje minusem
- podobne rozumowanie do wzoru na drogę:
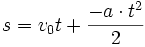
Nie stworzyliśmy nowych wzorów, a jedynie wprowadziliśmy poprawkę do poprzednich (w ruchu opóźnionym przyspieszenie bywa przeciwnie skierowane, dlatego wstawiamy minus; nadobowiązkowo zawsze występuje szybkość początkowa).
Ciało osiąga szybkość równą zero (zatrzymuje się) po czasie tk, tzn. w chwili końca ruchu.
Czas zatrzymania się
Ciało z przyspieszeniem przeciwnym do kierunku ruchu zaczyna zwalniać, do momentu zatrzymania. Jeśli interesuje nas, gdy organizm się zatrzyma, wystarczy iż przekształcimy wzór na szybkość (uwzględniając, iż w takiej chwili zatrzymane organizm posiada szybkość v=0):
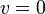

- wektor a posiada nieprzychylny zwrot, zmienia się znak:
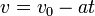
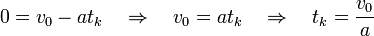
Dodatkowe wzory
Jeśli ze wzoru
wyznaczymy t i podstawimy do czasu w równaniu
 ,
,
to po przekształceniach otrzymamy tak zwane równanie bez czasu:
Wzór ten znajduje zastosowanie w obu ruchach - przyspieszonym i opóźnionym. W ruchu opóźnionym szybkość końcowa bywa mniejsza od początkowej, co sprawi, iż lewa strona równania będzie ujemna (tym samym jednocześcnie prawa), co oznacza, iż z prawej strony ujemne będzie przyspieszenie, a więc drgnienie będzie opóźniony.
Wzór ten możemy wykorzystać do wyprowadzenia kolejnego. Wyznaczmy więc s:
Jest on prawdziwy do ruchu przyspieszonego z prędkością początkową. W ruchu przyspieszonym bez prędkości początkowej (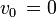 ) wzór przyjmuje postać:
) wzór przyjmuje postać:
Podobnie w ruchu opóźnionym, w którym szybkość końcowa równa bywa zero, podstawienie zera uprości wzór do jednej prędkości (jak powyżej).
Zadania
Zad. 1 (przyspieszenie) Pocisk wystrzelony z karabinu porusza się z przyspieszeniem 500 km/s2 i prędkością początkową 800m/s. Oblicz, jaką przebędzie odległość w ciągu 0,1 sekundy.
dane
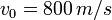
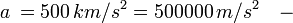 zamiana na jednostki podstawowe
zamiana na jednostki podstawowe
rozwiązanie
- Odległość policzymy ze wzoru na drogę; pocisk miał aczkolwiek szybkość początkową, którą również uwzględniamy:
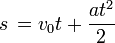
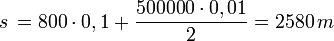
Wykonajmy nadobowiązkowo obliczenia na jednostkach, w celu sprawdzenia:
- szkic:
![\left [\tfrac{m}{s} \right ] \cdot [s] + \frac{\left [\tfrac{m}{s^2} \cdot s^2 \right ]}{[-]} \;=\; [m] + [m] = [m]](http://upload.wikimedia.org/math/7/1/4/714346f0aa2b4fea613b7c2f74ba00ac.png)
Ruch jednostajny prostoliniwy, definicja, wyjaśnienie, ogólnie.
| Definicja - Ruch jednostajny, prostoliniowy |
| Ruch ze stałą (co do wartości i kierunku) prędkością. |
- Tor ruchu jest linią prostą.
- Szybkość tego ruchu w każdym tego momencie bywa stała.
We wszystkich obliczeniach związanych z takim ruchem będziemy używać jednego wzoru: (postać wektorowa i 'uproszczona')

- Oznaczenia: s - droga, r - wektor drogi, t -czas.
UWAGA! Należy zaznaczyć, że pojęcie prędkość odnosi się do wektora, zaś pojęcie szybkości związane jest ze skalarem - wartością predkości.
Przyda się rozumieć - po co bywa i czemu tak bywa przedstawiona wersja wektorowa - tak naprawdę jest to definicja prędkości. Zapisaliśmy w niej dwa wektory - prędkości i przemieszczenia. Widzimy, że kierunek i zwrot wektora prędkości bywa ten sam co przemieszczenia. Jest to więc dodatkowa (choć intuicyjna) do nas informacja. Tak więc, dzięki zapisowi wektorowemu wiemy, jak znaleźć wektor prędkości jeśli odnajdziemy jej kierunek ze zwrotem.
W większości zadań z ruchem jednostajnym prostoliniowym możemy pomijać wzmiankę o kierunku i zwrocie prędkości, skoro się nie zmieniają. Dlatego - do łatwości posługiwania się - będziemy używać zwykłej formy bez wektorów, 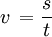 .
.
Ponadto, wzór możemy rozszerzyć do zapisu:
Znowu ukryta bywa tu dodatkowa informacja. Jaka? Delta ? oznacza zmianę lub przyrost. Co to może zmienić w naszych obliczeniach? W pewnych zadaniach nie możemy postawić każdego napotkanego czasu, a wyłącznie konkretny przedział - w którym drgnienie się odbywa. Podobnie z drogą, bierzemy pod uwagę odcinek, do którego obliczamy prędkość.
Przyjrzyjmy się zadaniu o treści:
"Jadący samochód znajdował się o godz. 10.00 w odległości 10km od stacji benzynowej. Jadąc w tutejszym samym kierunku, o godzinie 11.00 oddalił się już na odległość 15km od stacji. Oblicz szybkość w tutejszym ruchu." Jak powinniśmy interpretować te dane?
Zgodnie z poprzednimi zaleceniami, bierzemy zmianę drogi - samochód przebył 5 km. Trwało to 1 godzinę, bo o tyle zmienił się czas. Nie bywa to wymyślone, a zawiera się w naszym wzorze - wyrażenie zmienić się bywa symbolizowane u nas poprzez deltę.
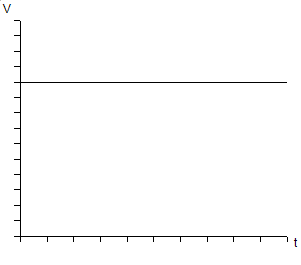
Wykres prędkości, tzn. zależność prędkości od czasu:
- Prędkość bywa stała (v = const).
Równanie i wykres drogi
Ciało w naszym ruchu przebywa pewną drogę, którą możemy policzyć z odpowiedniego wzoru. Przekształcając wzór na szybkość otrzymamy:
W niektórych przypadkach, zamiast o drodze - mówimy o położeniu ciała. Z reguły dowiadujemy się, iż organizm to znajdowało się początkowo w odległości x0, po czym poruszało się z prędkością v poprzez termin t. Znając te wielkości, możemy podać, w jakiej odległości (od jakiegoś miejsca) organizm znajduje się po wykonaniu ruchu - obliczamy, jaką drogę pokonało i dodamy początkową odległość. Można to oczywiście zobrazować wzorem: (dla rozróżnienia, drogę zamienimy takim łącznie na x - położenie)
Drogę i położenie możemy używać zamiennie - dają nam przecież tę samą informację, tzn. o jaką odległość przemieściło się ciało.
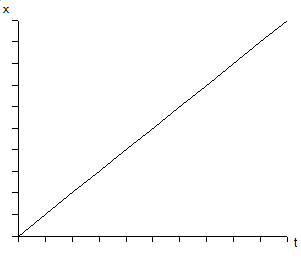
Na wykresie przedstawimy, jeśli zmienia się położenie ciała w kolejnych sekundach ruchu (wiąże się to oczywiście ze wzorem v=s/t).
- Położenie ciała bywa proporcjonalne do czasu (x ~ t).
Zadania
Fizyka uczy, jak pojmować zachodzące wokół nas zjawiska. Rozwiązując zadania dotyczące takich zjawisk, możemy uporządkować naszą wiedzę.
Zad.1 (odległość)
Z miejscowości A jedzie motor z szybkością v1=20 m/s. W chwili, gdy znajduje się w odległości x0=5 km od A, na tę samą trasę wjeżdża samochód z szybkością v2=90 km/h. Po jakim czasie i w jakiej odległości od A oba pojazdy się spotkają?
dane
- Oba pojazdy jadą pewną drogą, wiemy, iż w określonej chwili motor był w odległości 5km od startu, w którym znajdował się jadący samochód. Jednostka bywa niepoprawna, zamieniamy na metry.
- motor: xm0=5000m
- samochód: xs0 = 0m
- Prędkości obu pojazdów z poprawną jednostką (1 km/h = 1000m/3600s).
- v1 = 20 m/s
- v2 = 90 km/h = 90 (1000m/3600s) = 90000/3600 m/s = 25 m/s
rozwiązanie
- Potrzebny nam wzór:
- Podstawiamy dane (odległość początkowa, szybkość i nieznany termin ruchu t) do motocykla i samochodu, uzyskując równania:
- motocykl: x = 5000 + 20 t
- samochód: x = 0 + 25 t
- Czas t bywa ten sam do obu pojazdów, skoro liczymy go od konkretnej chwili do momentu ich spotkania.
- Wiemy też, iż spotkają się w tej samej odległości xod miejscowości A. Skoro te wielkości są równe, to zapiszemy:
- 5000 + 20 t = 0 + 25t
- 5000 = 5t
- t = 1000
- Trzymaliśmy się podstawowych jednostek, dlatego po obliczeniach jednostką t są sekundy. Podstawiamy t i obliczamy x.
- x = 5000 + 20 t
- x = 5000 + 20000 = 25000m
odp.
- Samochód i motocykl spotkają się w odległości 25000 metrów po czasie 1000 sekund.
Zad.2 (średnia szybkość)
Samochód przejechał trasę pomiędzy dwoma miastami. Pierwsze 20km poruszał się z szybkością 36km/h, a kolejne 40km z szybkością 40 m/s. Oblicz średnią szybkość samochodu.
dane
- s1=20000 m, s2=40000 m
- v1= 36 (1000m/3600s) = 10 m/s, v2 = 40 m/s
rozwiązanie
- Korzystamy ze wzoru s = v t. Nie wiemy, ile czasu poruszał się z podanymi szybkościami.
- 20000 = 10 t1 t1=2000 s
- 40000 = 40 t2 t2=1000 s
- Do policzenia średniej prędkości potrzebna nam bywa cała długość trasy i całkowity czas:
- vśr = s/t
- s = s1 + s2 = 60000 m
- t = t1 + t2 = 3000 s
- vśr = s/t = 20 m/s
odp.
- Średnia szybkość wynosiła 20 m/s.
Zad.3 R (względna prędkość)
Dwa samochody poruszają się do tego samego punktu. Wektory ich prędkości są prostopadłe i posiadają wartości adekwatnie 30 km/h i 40 km/h. Oblicz ich względną prędkość.
dane
- Jednostki zostają (nie będziemy w zadaniu przeprowadzać działań na jednostkach).
- v1=30 km/h, v2=40 km/h
rozwiązanie
- Obliczyć musimy względną prędkość, czyli:
- Co nie bywa trywialne, bo wektory posiadają różne kierunki. Wynikiem będzie trzeci wektor v, pokazany na rysunku (korzystamy z geometrycznego dodawania wektorów).
- Aby policzyć cena uzyskanego wektora v, możemy skorzystać z twierdzenia Pitagorasa.
- 302 + 402 = v2
- v2 = 2500
- v = 50 km/h
odp.
- Względna szybkość posiada cena 50 km/h.
Ciekawostki
Bo fizyką trzeba się bawić.
Porównajmy niektóre szybkości:
- jadący samochód: ok. 15-30 m/s
- szybkość dźwięku w powietrzu: ok. 340 m/s
- samolot Concorde: do 600 m/s
- Księżyc wokół Ziemi: ok. 1000 m/s
- pierwsza szybkość kosmiczna: ok. 7910 m/s (prędkość na orbicie okołoziemskiej)
- trzecia szybkość kosmiczna: ok. 16700 m/s (aby potrafić opuścić Układ Słoneczny)
- prędkość fal, światła: ok. 300000000 m/s
Według teorii A. Einsteina, szybkość światła bywa prędkością graniczną i nie możemy jej przekroczyć. Co więcej, gdy organizm porusza się prędkością zbliżoną do niej, tego masa się zmienia, a termin zaczyna cieknąć oryginalnie aniżeli w otoczeniu...
Wzory
Ile wzorów trzeba zapamiętać, żeby umieć opisać ruch jednostajny prostoliniowy? Pokażemy, iż żadnego.
Szybkość średnia
- Wzorem bywa v=s/t. Wystarczy aczkolwiek przypomnieć sobie jednostkę - km/h lub m/s. Podstawmy słowny opis: trasa / czas - i już mamy wzór na prędkość, którego nie trzeba zapamiętywać.
Droga
- Wzór w zrozumiały metoda wyprowadzamy ze wzoru na prędkość. (Można sprawdzić poprawność dzięki działaniom na jednostkach: m = m/s
 s, czyli droga=prędk
s, czyli droga=prędk  czas)
czas)
Czas
- Wzór jednocześnie wyprowadzamy ze wzoru na prędkość.
Można wspomnieć o przyspieszeniu - aczkolwiek posiada ono wartość zero, dlatego pojawia się dopiero w następnym rozdziale. To wszystko z ruchu jednostajnego.
Podstawy dotyczące ruchu ciał
Kinematyka ? dział mechaniki zajmujący się opisywaniem ruchów ciał; pomijając same przyczyny tych ruchów (np. siły).
Ruch
Ruch bywa wysoce powszechnym zjawiskiem, dlatego warto zapoczątkować od poznania sposobów tego opisu. Aby mówić, iż organizm się porusza, musimy odnaleźć do niego punkt odniesienia. Jadący samochód porusza się względem Ziemi i względem samolotu, choć z inną prędkością. Co więcej, jadące obok niego, z tą samą prędkością, auto już się względem niego nie porusza. To dowodzi, iż ruch bywa względny.
| Definicja - Ruch |
| Ruch bywa to zmiana położenia ciała względem innego ciała lub układu ciał zwanego układem odniesienia |
| Definicja - względność ruchu |
| Względność obserwowanego ruchu bywa na tym, iż drgnienie możemy obserwować wyłącznie względem danego układu odniesienia. |
Przykład
Na rzece płyną dwa kajaki. Jeden z nich płynie zgodnie z jej nurtem, drugi w przeciwnym kierunku. Zakładamy, iż wioślarze pracują w tutejszym samym tempie, tzn. tak samo napędzają swoje kajaki. W takim razie, kajaki poruszają się z tą samą prędkością względem płynącej wody.
Jak na ten drgnienie wpływa nurt rzeki? Dla zewnętrznego obserwatora okaże się, iż jeden kajak płynie znacznie szybciej, podczas gdy drugi ledwo się przemieszcza. Kajaki poruszają się tak samo względem wody, czy również np. względem płynącej w dół rzeki belki. Jednak względem Ziemi drgnienie kajaków bywa różny - jeden kajak zostaje 'przyspieszony', drugi 'spowolniony' poprzez działanie nurtu rzeki.
Widać, iż prędkości kajaków będą opisane oryginalnie względem płynącej wody, a oryginalnie względem Ziemi (i, oczywiście, oryginalnie względem ich samych nawzajem).
Układ odniesienia
W poprzednim przykładzie rozróżnialiśmy dwa układy odniesienia - płynącą wodę i Ziemię. Widać było, iż ten sam drgnienie bywa opisany oryginalnie w każdym z nich.
Człowiek stojący na Ziemi nie porusza się względem niej. Jednak nie oznacza to, iż w ogóle się nie porusza - wystarczy zmienić układ odniesienia, i już możemy powiedzieć, iż porusza się on względem Słońca, czy względem innej galaktyki. Jeśli obierzemy samochód za układ odniesienia, pasażerowie się nie poruszają, choć budynki na ulicy już tak. Nie możemy powiedzieć, iż budynki 'stoją w miejscu' lub iż spoczywają - a jedynie, iż spoczywają względem Ziemi.
Na wykresach za układ odniesienia służy nam układ 2 osi X i Y.
Droga i przemieszczenie
Tor
- Ślad jaki zostawia po sobie poruszający się obiekt.
Droga
- Czyli długość toru, po jakim organizm się poruszało. Jest określone poprzez równanie toru - wzór związany od kształtu toru (odcinek, łuk, parabola itd).
Przemieszczenie
- Jeśli połączymy początkowy i docelowy punkt drogi, którą przebyło ciało, otrzymamy wektor przesunięcia (przemieszczenia) ciała. Inaczej mówiąc bywa to zmiana położenia.
Położenie
- Usytuowanie obiektu względem układu odniesienia, którym mogą istnieć inne obiekty. Położenie obiektu możemy określić za pomocą układu współrzędnych.
Przyjrzymy się ruchowi dziecka na karuzeli. Załóżmy, iż karuzela wykonała pełny obrót - wówczas położenie końcowe dziecka pokrywa się z początkowym. Dziecko pokonało pewną drogę, aczkolwiek wektor przesunięcia bywa zerowy.
Będziemy ich używać intuicyjnie, możemy powiedzieć - nieświadomie. Droga posłuży nam w obliczeniach, dokąd używamy wartości przebytej drogi. Przemieszczenia natomiast użyjemy, gdy będziemy potrzebowali graficznego opisu drogi - te informacje zawiera wektor przemieszczenia.
Możemy jednocześcnie wyróżnić wielkość: położenie ciała w ruchu - bywa to po prostu odległość ciała od tego położenia początkowego.
Prędkość
Opisuje, jeśli prędko porusza się organizm - czyli jaką drogę pokonuje w określonym czasie. Taki również bywa wzór: cena prędkości = trasa / czas. Działania na jednostkach są analogiczne, jednostką podstawową bywa m/s.
Pociąg, jaki przebył odległość 400m w czasie 20s poruszał się z prędkością 20m/s. Jednak, gdyby zatrzymał się i ruszył w przeciwnym kierunku znów z prędkością 20m/s, jeśli byśmy ją opisali? Jej cena bywa taka sama, aczkolwiek skierowana bywa w przeciwnym kierunku.
Podsumowując, gdy drgnienie bywa skomplikowany, potrzebujemy działań na wektorach, użyjemy wektora prędkości (aby zważać kierunek i zwrot). W obliczeniach używać będziemy samej wartości. Dla ułatwienia, prostsze ruchy jednocześcnie opisywać będziemy jedynie wartościami (skalarami).
W praktyce organizm porusza się ruchem niejednostajnym - raz zwalnia, raz przyspiesza. Prędkość policzona ze wzoru będzie mało dokładna. Możemy przyjąć, iż cały termin opisywana szybkość to prędkość średnia. Wyróżniamy jednocześcnie prędkość chwilową - bywa to szybkość zmierzona w wysoce krótkim czasie, poprzez co dość drobiazgowo odzwierciedla drgnienie w konkretnej chwili.
Czasem rozróżnia się szybkość i szybkość - ta pierwsza bywa używana jako wektor, natomiast szybkość jako cena skalarna.
Prędkość względna
Obliczenia na prędkościach dwóch ciał w celu policzenia ich prędkości względnej.
Prosta reguła:
- Jeśli ciała poruszają się w tę samą stronę, prędkości odejmujemy (jadące w jedną stronę samochody z prędkościami 80km/h i 60km/h, jeden od drugiego oddala się z prędkością 20km/h)
- Jeśli ciała poruszają się naprzeciw siebie, prędkośći dodajemy (jadące naprzeciw siebie samochody o prędkościach 80 i 60 km/h - posiadają szybkość względną 140km/h)
Rozwinięcie
Precyzyjniej szybkość względną możemy obliczyć z wektorów (np. gdy 2 ciała poruszają się względem siebie pod pewnym kątem). Jest to po prostu odmienność wektorów prędkości. Pewna trudność ukazuje się aczkolwiek w liczeniu różnicy wektorów.
Jeżeli dodajemy lub odejmujemy wektory, nie możemy tego zrobić bezpośrednio - gdy ich kierunki się nie pokrywają, sięgamy po funkcje trygonometryczne. Więcej szczegółów możemy odnaleźć w zadaniach rozszerzonych.
Rodzaje ruchu
Rodzaj ruchu rozróżniamy ze względu na forma tego toru i metoda zmiany prędkości.
Ruch może być:
- prostoliniowy (wzdłuż prostej)
- krzywoliniowy (np. drgnienie po okręgu)
Oraz, w zależności od prędkości:
- jednostajny (prędkość nie zmienia się)
- jednostajnie zmienny: przyspieszony lub opóźniony (prędkość zmienia się o stałą wartość)
- niejednostajnie zmienny (prędkość zmienia się o różne wartości)
Przykład
| Przykład - |
| Startujący samolot może ruszać się ruchem jednostajnie przyspieszonym, prostoliniowym, jeżeli tego szybkość rośnie o stałą cena i porusza się w linii prostej. |
Mechanika kwantowa - podstawy zadanie 9 - cząstka alfa w jednorodnym polu magnetycznym
Cząstką alfa porusza się w próżni po okręgu o promieniu R=5cm w jednorodnym polu magnetycznym o indukcji B=2,5 * 10^-2 T.
Obliczyć długość fali materii odpowiadającą tej cząstce.
Zobacz rozwiązanie! - kliknij na napis "więcej" znajdujący się poniżej.
Mechanika kwantowa podstawy zadanie 7 laser emituje fotony
Laser CO2, charakteryzuje się bardzo dużą mocą.
Emituje światło podczerwone o długości fali lambda=10mikrometrów
Oblicz, ile fotonów na sekundę emituje laser CO2 o mocy P=1kW
Zobacz rozwiązanie! - kliknij na napis "więcej" znajdujący się poniżej.
Mechanika kwantowa - podstawy zadanie 6 - efekt fotoelektryczny
a) Na czym polega zjawisko fotoelektryczne
b) Jaką energię kinetyczną mają elektrony wybite z metalu pod wpływem promieniowania nadfioletowego o długości lambda=10^-7 m ?
Częstotliwość graniczna wynosi 10^15 Hz.
Zobacz rozwiązanie! - kliknij na napis "więcej" znajdujący się poniżej.
Mechanika kwantowa - podstawy zadanie 5 - Atom Wodoru
a)Oblicz energię fotonu podczas przejścia elektronu w atomie wodoru z orbity 4 na 2.
b) Foton ten jest pochłonięty czy emitowany ?
Zobacz rozwiązanie! - kliknij na napis "więcej" znajdujący się poniżej.
Mechanika kwantowa - podstawy zadanie 4 - Czy atom wodoru , który znajduje się w stanie podstawowym może pochłonąć foton o energii 14eV ?
Czy atom wodoru , który znajduje się w stanie
podstawowym może pochłonąć foton o energii 14eV ?
Zobacz rozwiązanie! - kliknij na napis "więcej" znajdujący się poniżej.
Mechanika kwantowa - zadanie 3 - I postulat Bohra
a)Napisz I postulat Bohra dotyczący atomu wodoru.
b) Promień drugiej orbity elektronu w atomie wodoru
wynosi r2=2,1*10^-10m. Stosując warunek jaki spełniają
orbity dozwolone oblicz jaka jest prędkość elektronu tej orbicie?
Zobacz rozwiązanie! - kliknij na napis "więcej" znajdujący się poniżej.

 dr inż. Paweł Troka
dr inż. Paweł Troka