Korepetycje
Polecane książki
|
|

dr inż. Paweł Troka
Owner & CEO
E-Mail: ptroka@fizyka.dk
PTroka on Google+
Kinematyka - Ruch Jednostajnie Przyśpieszony - zadanie 4
Czas reakcji przeciętnego kierowcy wynosi około 0,7 s (czas między momentem
zauważenia przez kierowcę sygnału STOP, a momentem naciśnięcia na hamulec). Wiedząc, że
hamujący samochód uzyskuje przyspieszenie a = -4 m/s2, znajdź całkowitą odległość przebytą
przez pojazd od zauważenia sygnału STOP do zatrzymania się, gdy wartość jego prędkości
wynosi 162 km/h.
Zobacz rozwiązanie, kliknij "więcej" !
Zbiór zadań przygotowujących do matury rozszerzonej z fizyki
Zbiór to unikalne połączenie minimalnej prosto wyłożonej teorii z wieloma zadaniami (maturalnymi i nie tylko) wraz z pełnymi rozwiązaniami.
Zadania pochodzą z różnych źródeł, główny nacisk położony został jednak na to, abyś drogi czytelniku dzięki temu zbiorowi przygotował się do matury z fizyki na poziomie rozszerzonym.
Na poziom rozszerzony dobraliśmy zadania wyjątkowo starannie, posegregowaliśmy je w zbiorze w działy, aby wygodniej było się Tobie uczyć i przygotowywać do matury.

Zbiór składa się z działów:
- Kinematyka
- Dynamika
- Ruch obrotowy bryły sztywnej
- Pole grawitacyjne, Praca, Moc, Energia
- Elektrostatyka
- Prąd stały
- Pole magnetyczne
- Indukcja elektromagnetyczna i prąd zmienny
- Termodynamika
- Hydrostatyka
- Ruch drgający i falowy
- Optyka i fale elektromagnetyczne
- Falowe właściwości materii i cząsteczkowe właściwości światła
- Fizyka jądrowa
- Astronomia
Można go zobaczyć lub pobrać, źródła z których można pobrać ułożono od najszybszych do najwolniejszych:
wersja nr 1 - PDF bez kompresji w wysokiej jakości:
zobacz: Zbiór zadań przygotowujących do matury rozszerzonej z fizyki z rozwiązaniami - PDF
pobierz(zalecamy pobranie, gdyż będziasz miał plik na dysku): źródło 1 | źródło 2 | źródło 3 | źródło 4
wersja nr 2 - skompresowany PDF:
zobacz: Zbiór zadań przygotowujących do matury podstawowej z fizyki z rozwiązaniami - PDF
Zbiór zadań przygotowujących do matury podstawowej z fizyki
Zbiór to unikalne połączenie minimalnej prosto wyłożonej teorii z wieloma zadaniami (maturalnymi i nie tylko) wraz z pełnymi rozwiązaniami
Zadania pochodzą z różnych źródeł, główny nacisk położony został jednak na to, abyś drogi czytelniku dzięki temu zbiorowi przygotował się do matury z fizyki na poziomie podstawowym.
Można go zobaczyć lub pobrać, źródła z których można pobrać ułożono od najszybszych do najwolniejszych:
wersja nr 1 - PDF bez kompresji w wysokiej jakości:
zobacz: Zbiór zadań przygotowujących do matury podstawowej z fizyki z rozwiązaniami - PDF
pobierz(zalecamy pobranie, gdyż będziasz miał plik na dysku): źródło 1 | źródło 2 | źródło 3 | źródło 4
wersja nr 2 - skompresowany PDF:
zobacz: Zbiór zadań przygotowujących do matury podstawowej z fizyki z rozwiązaniami - PDF
15 zbiorów zadań przygotowujących na sprawdzian czy kartkówkę z poszczególnych działów fizyki
Zadania pochodzą głównie z egzaminów maturalnych, ale nie tylko.
Jako że są podzielone na działy stanowią wygodne źródło zadań na naukę przed sprawdzianem czy pracą klasową, większość zadań ma odpowiedzi.
Polecamy!

Nieskompresowane PDF (ładna jakość):
1. Kinematyka
2. Dynamika
3. Ruch obrotowy bryły sztywnej
4. Pole grawitacyjne. Praca. Moc.Energia
5. Pole elektrostatyczne
6. Prad elektryczny
7. Pole magnetyczne
8. Indukcja elektromagnetyczna. Prąd przemienny
9. Termodynamika
10. Hydrostatyka
11. Ruch drgający i fale mechaniczne
12. Fale elektromagnetyczne
13. Korpuskularne właściwości światła i falowe właściwości materii
14. Fizyka jądrowa
15. Astronomia
Zebrane w jeden plik PDF
Można go zobaczyć lub pobrać, źródła z których można pobrać ułożono od najszybszych do najwolniejszych:
wersja nr 1 - PDF bez kompresji (dobra jakość):
zobacz: 15 zbiorów zadań z fizyki dla liceum JEDEN PLIK
pobierz(zalecamy pobranie, gdyż będziasz miał plik na dysku): źródło 1 | źródło 2 | źródło 3 | źródło 4
wersja nr 2 - skompresowany PDF (znacznie gorsza jakość)
zobacz: 15 zbiorów zadań z fizyki dla liceum JEDEN PLIK
pobierz(zalecamy pobranie, gdyż będziasz miał plik na dysku): źródło 1 | źródło 2 | źródło 3 | źródło 4
W jeszcze większej ilości zadania z fizyki z rozwiązaniami dla liceum i z matury.
 Nasz serwis powoli się rozrasta, powoli gdyż obecnie pracują przy nim zaledwie dwie osoby, a rozrasta się gdyż dodajemy dzisiaj ogromne zasoby edukacyjne.
Nasz serwis powoli się rozrasta, powoli gdyż obecnie pracują przy nim zaledwie dwie osoby, a rozrasta się gdyż dodajemy dzisiaj ogromne zasoby edukacyjne.
Z dniem dzisiejszym oprócz cały czas dostępnych przykładowych zadań z fizyki z rozwiązaniami dla każdego działu (nie mamy jeszcze ich wiele ale są na bieżąco dodawane) - zadania z fizyki z rozwiązaniami, do materiałów dostępnych w serwisie dodajemy unikalne i bardzo obszerne zbiory zadań z fizyki - darmowe zbiory zadań z fizyki z rozwiązaniami dla liceum i z matury.
W tym powyższym nowym dziale już na starcie możesz drogi czytelniku, pobierać zbiory z trzech kategorii, są to:
- zbiór zadań przygotowujący do matury podstawowej z fizyki
- zbiór zadań przygotowujący do matury rozszerzonej z fizyki
- 15 zbiorów zadań przygotowujących na sprawdzian czy kartkówkę z poszczególnych działów fizyki
To naprawdę sporo, wraz z naszymi innymi materiałami takimi jak przykładowe zadania z rozwiązaniami, teoria, poradniki i symulacje zjawisk fizycznych które wkrótce zamieścimy masz u nas wszytsko co potrzebne Ci aby przygotować się do matury z fizyki.
Pozdrawiamy!
v0.21pre-alpha Opis i cechy fali mechanicznej, Fala biegnąca
Opis i cechy fali mechanicznej
W ośrodku sprężystym rozchodzi się fala mechaniczna jeśli element ośrodka jest wytrącany cyklicznie z położenia równowagi.
Cechy fali biegnącej
długość - odległość jaką przebywa fala w danym okresie
częstotliwość i okres - są równe częstotliwości i okresowi źródła drgań wytwarzającemu fale
Jeżeli źródło fali jest oscylatorem harmonicznym to powstaje fala sinusoidalna.
amplituda - maksymalne wychylenie cząsteczki fali z położenia równowagi
prędkość - jest cechą ośrodka
Rodzaje fal:
- poprzeczne
- podłużne
- koliste
- płaskie
- kuliste
Równania opisujące falę biegnącą
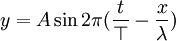
t - chwila czasu, w której określono wychylenie z położenia równowagi
x - odległość danego punktu od początku układu współrzędnych
? - długość fali

Faza fali biegnącej: argument funkcji sinus.
Ruch harmoniczny, definicje, ciało na sprężynie
Ruch harmoniczny, definicje
1. Ruch w którym siła wprawiająca ciało w ruch jest proporcjonalna do wychylenia i ma zwrot przeciwny do wychylenia
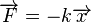
k - współczynnik charakteryzujący oscylator
x - wychylenie z położenia równowagi
2. Ruch, w którym wychylenia z położenia równowagi zmieniają się zgodnie ze zmianą funkcji sinus, czyli są sinusoidalnie zmienne
x(t) = Asin(?t + ?)
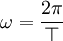
A - amplituda
? - częstość kołowa
? - faza początkowa ruchu (kąt wychylenia z położenia równowagi w chwili rozpoczęcia pomiaru czasu)
Równania ruchu oscylatora harmonicznego
- oznaczenia :
x - wychylenie ze stanu równowagu ( położenia zero )
A - amplituda drgań ( maksymalne wychylenie )
T - okres, jednostka [s]
? - częstość drgań, jednostka [Hz,1/s]
? - przesunięcie fazowe
- związki :
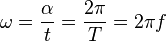
- ponieważ ? jest wyrażone w radianach.
Ponadto nie powinno używać się do opisu częstości kołowej jednostki Hz (chociaż jest to poprawne). Preferowany zapis: s ? 1
- położenie (przemieszczenie)
x = Asin(?t + ?)
- prędkość
V = Vmaxcos(?t + ?)
Vmax = ?A
- prędkość ( skąd to się bierze ;)
Prędosć jest pochodną położenia po czasie , więc :
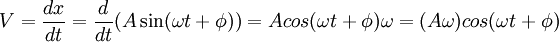
- przyspieszenie (zwrot siły wypadkowej)
a = ? amaxsin(?t + ?)
amax = ?2A
Związki dla ciężarka drgającego na sprężynie
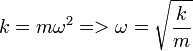
F = ? m?2Asin(?t + ?)
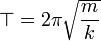
Siła, prędkość, przyspieszenie w ruchu harmonicznym
F = ? Asin(?t + ?)
?t + ? to tzw. faza
F = ? kx
? m?2 = Asin(?t + ?)
Opis zmian siły, prędkości, przyspieszenia
x = Asin(?t + ?)
V = ?Acos(?t + ?)
a = ? ?2Asin(?t + ?)
| czas | x | F | V | a |
| 0 | 0 | 0 | ?A | 0 |
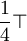 |
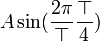 |
m?2A | 0 |  |
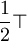 |
0 | 0 | ?A | 0 |
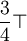 |
A | m?2A | 0 |  |
 |
0 | 0 | ?A | 0 |
Siła Bezwładności
Zgodnie z I zasadą dynamiki Newtona w układach inercjalnych, kiedy siły działające na ciało równoważą się pozostaje ono w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Zupełnie odmienna sytuacja zachodzi w układach nieinercjalnych, gdzie ciało przyśpiesza za sprawą przyspieszenia układu, choć nie działają na nie żadne niezrównoważone siły. Gdy układ przekazuje cialu swoje przyśpieszenie pojawia się siła kontrreakcji zwana właśnie bezwładnością. Stąd jej zwrot przeciwny jest do zwrotu przyśpieszenia układu.
Bezwładność ciał jest to ich zdolność do przeciwstawiania się wszelkim zmianom ruchu.
gdzie:
 - siła bezwładności
- siła bezwładności - przyśpieszenie układu
- przyśpieszenie układu- m - masa ciała
Wzór ten uwzględznia zwrot siły bezwładności.
Podróż windą
Dobrym przykładem ilustrującym występowanie siły bezwładności jest podróż windą. Kiedy rusza do góry z dużym przyspieszeniem czujemy się wbijani w podłogę. Z kolei gdy gwałtownie hamuje, że zaraz wzlecimy w powietrze. Podobnie jest ze zjeżdżaniem na dół. Kiedy winda zaczyna opadać, czujemy się unoszeni, zaś kiedy hamuje na dole, że "coś przyciska nas do podłogi". Dzieje się tak za sprawą działającej na nas siły bezwładności.
Analizując dane przykłady zastanówmy się jak zależy zwrot siły bezwładności od zwrotu przyspieszenia i prędkości.
W przypadku jazdy w górę:
- winda rusza - wektor przyspieszenia (ruch przyśpieszony) oraz prędkości windy skierowane ku górze, wektor bezwładności ku dołowi ("wbijanie w ziemię")
- winda hamuje - wektor przyśpieszenia windy skierowany ku dołowi (ruch opóźniony), wektor prędkości windy skierowany ku górze (bo winda mimo wszystko jedzie do góry), wektor siły bezwładności ku górze ("odrywamy się od podłogi")
Na tych dwóch przykładać widać już wyraźnie, że wektor prędkości nie wpływa na zwrot siły bezwładności. Wszak w obu przypadkach skierowany był ku górze, a zwrot siły bezwładności zmieniał się. Jasno dostrzegalny jest za to związek między zwrotem przyspieszenia a zwrotem siły bezwładności.
Siła bezwładności działa przeciwnie do zwrotu przyśpieszenia
W ramach powtórzenia i lepszego zrozumienia zagadnienia spróbuj samodzielnie przeanalizować zwroty prędkości, przyśpieszenia i siły bezwładności podczas jazdy w dól.
Sily pozorne
Jak już mówiliśmy we wstępie siła bezwładności ściśle związana jest z układami nieinercjalnymi - takimi, w których ciało przyśpiesza ponieważ przyśpiesza jego układ.
Gdy stojący samochód gwałtownie zaczyna się poruszać czujemy się wbijani w oparcie fotela. Jednak raz wprawiona w ruch maszyna poruszająca się ruchem jednostajnym nie wywołuje już takich reakcji. Dlaczego? Dzieje się tak ponieważ w pierwszym przypadku znajdujemy się w układzie odniesienia posiadającym własne przyśpieszenie, a co za tym idzie nadającym nam siłę pozorną. Gdy układ przekazuje nam swoje przyśpieszenie pojawia się siła bezwładności - kontrreakcji. Stąd jest ona skierowana przeciwnie do zwrotu przyśpieszenia układu.
Do sił pozornych należy nie tylko bezwładność ale też siły odśrodkowa i dośrodkowa występujące gdy ciało porusza się po łuku. Ruch po okręgu należy do układów nieinercjalnych, gdyż występuje w nim przyśpieszenie dośrodkowe.
Efekt Coriolisa
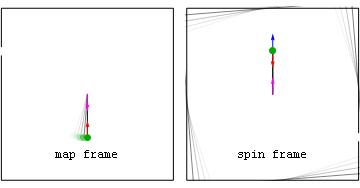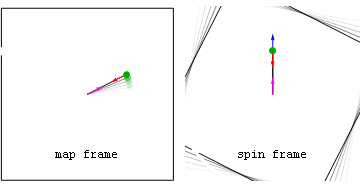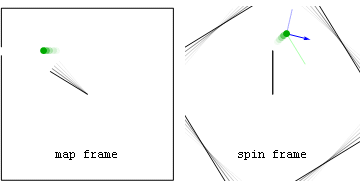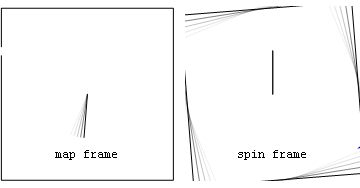
Efekt Coriolisa podobnie jak siła bezwładności działa jedynie w układach nieinercjalnych. Dla obserwatora znajdującego się w obracającym się układzie odniesienia tor ruchu ciał znajdującego się w tym samym układzie jest zakrzywiony. Dzieje się tak za sprawą pozornej siły Corolisa.
Pierwsza ramka przedstawia obiekt z perspektywy osoby pozostającej w bezruchu. W drugim przypadku uklad ukazany jest oczyma obserwatora znajdującego się w obracającym się układzie.
Siły w ruchu po okręgu
Działające na ciało poruszające się po łuku siły odśrodkowa i dośrodkowa są siłami bezwładności, więc również należą do sił pozornych. 
Do zrobienia:
|
I zasada dynamiki
I zasada dynamiki
Dynamika - wstęp
Dynamika, podobnie jak kinematyka, opisuje ruch ciała, uwzględnia jednak przyczyny tego ruchu.
Początkowo, przyczyny ruchu próbował opisać Arystoteles. Zauważył on, że ciało dąży do bycia nieruchomym, a porusza się jedynie, gdy działa na nie jakaś siła. Ziemię uważano za środek wszechświata, do tego za zupełnie nieruchomą. Każde inne ciało do ruchu potrzebowało 'ciała popychającego'. Teorie te przekreśliło jednak dzieło Kopernika - mówiące, że to Ziemia porusza się wokół Słońca. Wynikało z tego, że planety poruszają się mimo braku 'popychającej siły'. Wbrew obserwacjom, okazuje się, że naturalnym stanem ciała nie jest spoczynek, ale właśnie ruch.
Pierwsza zasada dynamiki
Kolejny uczony - I. Newton - opisał przyczyny ruchu trzema zasadami dynamiki. Pierwsza zasada dynamiki Newtona mówi, że prędkość ciała nie zmienia się, jeśli nie działa na nie żadna siła.
- I zasada dynamiki: Ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym, jeśli nie działa na nie żadna siła, lub suma sił wynosi zero.
Musimy z tego pamiętać, że jeśli ciało ma się zacząć poruszać lub zmienić prędkość, musi zadziałać siła. I odwrotnie, jeśli nie działa żadna (wypadkowa) siła, ciało nie porusza się lub porusza się ruchem jednostajnym.
Podsumowanie - jeśli ciało porusza się i przyspiesza, to działa na nie jakaś siła. Jeśli ciało porusza się i zwalnia, również działa na nie jakaś siła (głownie siła tarcia - np. podłogi, asfaltu itd.). Jeśli ciało porusza się bez zmiany prędkości, to znaczy, że nie działa żadna siła - lub suma sił wynosi zero (co oznacza, że się równoważą).
Zasada ta tłumaczy nam, skąd się wziął błąd w teorii Arystotelesa ("naturalnym stanem ciała jest spoczynek"). Weźmy przykład: przedmiot, na który ktoś działa siłą, porusza się w pewien sposób. Jednak, jeśli siła od tej osoby przestanie występować, przedmiot powinien nadal poruszać się ruchem bez zmiany prędkości. Dlaczego więc dowolna, przesunięta czy popchnięta rzecz, po chwili się zatrzymuje? Spowodowane jest to tarciem - tarcie spowalnia ruch, aż do zatrzymania się. Jest siłą powodującą opóźnienie ruchu ciała. Dopiero gdyby pozbyć się siły tarcia, możemy powiedzieć, że nie występuje żadna siła i przedmiot będzie poruszał się w nieskończoność. Można przypomnieć sobie, jak poruszają się przedmioty po śliskiej powierzchni - jest małe tarcie, więc słabiej wpływa na ruch i przedmiot minimalnie hamuje. Więcej o sile tarcia w dalszych częściach podręcznika.
Układ inercjalny
Jak wiemy z względności ruchu, można powiedzieć, że ciało spoczywa, możemy równocześnie powiedzieć że się porusza - zależy, względem jakiego układu odniesienia to opiszemy. Na przykład, stojący człowiek nie porusza się względem Ziemi, ale porusza się względem Słońca. Również we wspomnianej zasadzie dynamiki musimy uwzględnić różnice w wyborze układu odniesienia.
I zasada dynamiki mówi nam, że ciało, na które nie działa siła lub siły te się równoważą, porusza się z ze stałą prędkością lub spoczywa. Wiemy jednak, że ruch jest względny, dlatego ruch ciała (porusza się i spoczywa) trzeba opisywać wobec konkretnego układu. Czy wobec wszystkich układów zasada ta jest spełniona? Okazuje się, że nie - dlatego wyróżniamy układy inercjalne (gdzie zasada ta zachodzi) oraz nieinercjalne (gdzie nie zachodzi).
Tak więc, pewne układy odniesienia są układami inercjalnymi - ruch ciała wobec tych układów spełnia I zasadę dynamiki. Mówi ona, że ciało nie zmienia swojej prędkości, jeśli nie działa na nie siła, czyli:
- jest w spoczynku lub
- porusza się ruchem jednostajnym
wobec dowolnego układu inercjalnego. Układy inercjalne poruszają się względem siebie ruchem jednostajnym oraz nie występuje nigdzie przyspieszenie. Jeżeli jakiś układ przyspiesza, staje się układem nieinercjalnym - ponieważ ciała znajdujące się w nim również poruszają się ruchem przyspieszonym, mimo braku oddziaływania siły.
Przykład
Pasażer znajduje się w jadącym ze stałą prędkością pociągu. Nie działa na niego żadna siła (lub siły równoważą się), więc nie porusza się względem pociągu, co jest zgodne z I zasadą dynamiki. Pociąg jest więc dla pasażera układem inercjalnym. Ponadto, pociąg jedzie ze stałą prędkością, więc mówimy, że porusza się wobec innych układów ruchem jednostajnym (np. względem Ziemi).
Co się stanie jednak, jeśli pociąg przyspieszy? Zacznie poruszać się ruchem przyspieszonym, a wówczas prędkość pasażera - mimo braku działającej na niego dodatkowej siły - zacznie się zmieniać. Przeczy to I zasadzie dynamiki, dlatego przyspieszający pociąg jest już układem nieinercjalnym.
Układ nieinercjalny występuje więc, jeśli I zasada dynamiki nie jest spełniona. Wówczas ciało w tym układzie może zmieniać szybkość, mimo że nie działa na nie żadna siła, lub nie zmieniać prędkości, nawet jeśli działa na nie jakaś siła. Spowodowane to jest tym, że układ nieinercjalny porusza się ruchem przyspieszonym względem układów inercjalnych.
Ruch jednostajny po okręgu
Ruch jednostajny po okręgu
Ciało porusza się ruchem jednostajnym i torem tego ruchu bywa okrąg.
| Definicja - Ruch jednostajny po okręgu |
| Ruch jednostajny po okręgu bywa przypadkiem ruchu krzywoliniowego, którego cena prędkości nie ulega zmianie. W ruchu występuje moc dośrodkowa, która powoduje powstanie przyspieszenia dośrodkowego(normalnego), jakie powoduje zmianę kierunku wektora prędkości. |
| Przykład - Ruchy po okręgu |
Najprostsze przykłady tego ruchu spotykane w życiu codziennym:
|
Jedną z cech tego ruchu bywa wielkość zwana okresem T. Jest to czas, w ciągu którego organizm pokonuje całą długość toru - czyli obwód koła. Oznacza to, iż po czasie T organizm wraca do 'punktu wyjścia'.
Czas jednego obrotu, czyli okres, możemy zamienić na inną wielkość - częstotliwość (częstość). Jest to liczba obrotów wykonanych w ciągu jednostki czasu. Przykładowo, wał w silniku może wykonywać 3000 obrotów na minutę.
- częstotliwość
![\nu\,=\frac{1}{T} \;\; [\mbox{Hz}] = \left [\frac{1}{s}\right ]\qquad -](http://upload.wikimedia.org/math/d/d/d/ddd881c07e9aac57a3fcf12b5eb897ee.png) zależność pomiędzy częstotliwością i okresem, jednostka Herc.
zależność pomiędzy częstotliwością i okresem, jednostka Herc.
Prędkość takiego ciała obliczamy jeśli w ruchu jednostajnym. Wiemy, iż drogę s równą obwodowi koła pokonuje w czasie równym okresowi, podstawmy te dane do wzoru.
- wartość prędkości liniowej (szybkość)
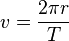
- wektor
 bywa styczny do okręgu.
bywa styczny do okręgu.
Prędkość liniowa bywa zawsze skierowana stycznie do okręgu - co oznacza, iż zwrot prędkości podczas ruchu cały termin się zmienia, cały termin bywa styczne do okręgu, poprzez co organizm 'zakreśla' okrąg. Jednak co wpływa na to, iż szybkość liniowa bywa cały termin styczna do okręgu ruchu? Przyczyną tego bywa przyspieszenie dośrodkowe, jakie omówione zostanie dalej.
Szybkość możemy uzewnętrznić jednocześcnie w odmienny sposób, przy pomocy kąta, jaki zakreśliło organizm poruszając się po okręgu w danym czasie. Jeśli punkt początkowy i docelowy ruchu połączymy liniami z środkiem okręgu, to linie te utworzą właśnie zakreślony poprzez organizm kąt  .
.
- szybkość kątowa
![\omega \,= \frac{\alpha}{t}\qquad \left [\frac{rad}{s} \right ] \mbox{lub} \left [\frac{1}{s} \right ]](http://upload.wikimedia.org/math/d/b/e/dbea09ac019069d7307dfa25c0f2bd9b.png)
Przykład
Satelita znajduje się w odległości 40000km od środka Ziemi, zawsze nad takim samym punktem Ziemi (porusza się 'równo' z planetą). Opiszmy ten ruch:
- 1. okres
 w takim czasie satelita wykona pełny obrót wokół Ziemi
w takim czasie satelita wykona pełny obrót wokół Ziemi
- 2. częstotliwość
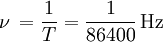
- Przebytą drogę obliczymy licząc obwód okręgu:
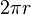 , dokąd r to promień okręgu. Promieniem bywa odległość satelity od środkowego punktu (środka Ziemi), drobiazgowo ten wymiar mamy podany w zadaniu.
, dokąd r to promień okręgu. Promieniem bywa odległość satelity od środkowego punktu (środka Ziemi), drobiazgowo ten wymiar mamy podany w zadaniu.
- 3. szybkość liniowa (v=s/t):
![v\,= \frac{2\pi r}{T} = \frac{2 \pi \cdot 40 000 000 }{86400}\, \left [\frac{m}{s} \right ] \qquad -](http://upload.wikimedia.org/math/3/7/2/372536af3a05ebf80a8dc22d4f821708.png) ze zmianą jednostek
ze zmianą jednostek
- Aby policzyć szybkość kątową, skorzystajmy z faktu, iż satelita przebędzie całą drogę w czasie równym okresowi T (wynika to z definicji okresu). Zakreśli przy takim kąt pełny, czyli 360o =
 .
.
- 4. szybkość kątowa
![\omega \,= \frac{\alpha}{t} = \frac{2\pi}{86400} \quad \left [\frac{rad}{s} \right ]](http://upload.wikimedia.org/math/6/0/c/60cabfe2038a77d1b976a1442ffadc00.png)
Warto wiedzieć, jeśli możemy obliczyć kąt, jaki zakreśla ciało. Jest to stosunek łuku s (łuk to droga, którą przebywa ciało) do promienia r:
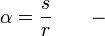 s to zakreślony łuk
s to zakreślony łuk
Dzięki temu możemy zapisać zależność pomiędzy prędkością kątową a prędkością liniową
- mając
 otrzymujemy zależność
otrzymujemy zależność 
- szybkość kątowa a liniowa:
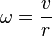
Przyspieszenie dośrodkowe
W ruchu po okręgu występuje siła dośrodkowa (więcej o siłach w dalszych częściach podręcznika), która nadaje ciału przyspieszenie dośrodkowe. Przyspieszenie to zmienia kierunek wektora prędkości, przy czym nie zmienia tego wartości.
Siłę tę możemy policzyć,  , gdzie: m - masa ciała, v - cena prędkości liniowej (szybkość), r - promień okręgu (toru ruchu). Siła ta bywa skierowana do środka okręgu.
, gdzie: m - masa ciała, v - cena prędkości liniowej (szybkość), r - promień okręgu (toru ruchu). Siła ta bywa skierowana do środka okręgu.
Przyspieszenie dośrodkowe ar bywa skutkiem działania siły dośrodkowej. Można je policzyć ze wzoru zawierającym szybkość liniową i promień okręgu:
Skierowane bywa jednocześcnie do środka okręgu. Jak już zostało wspomniane, przyspieszenie to powoduje zmianę kierunku wektora prędkości, tak by był cały termin styczny do toru ruchu, skutkiem czego organizm porusza się właśnie ruchem po okręgu. Nie zmienia wartości prędkości ciała, stąd drgnienie bywa jednostajny.
Podsumowanie
- ciało porusza się ruchem jednostajnym krzywoliniowym po okręgu o promieniu r
- okres T to odwrotność częstotliwości
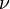
- wartość prędkości liniowej v (jak w ruchu jednostajnym) bywa równa drodze podzielonej poprzez czas. W szczególnym przypadku drogą może istnieć obwód koła 2?r, wówczas termin bywa gładki okresowi (
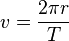 )
) - ciało po pewnym czasie zakreśla kąt
 , jaki możemy policzyć poprzez podzielenie przebytego łuku poprzez promień okręgu (
, jaki możemy policzyć poprzez podzielenie przebytego łuku poprzez promień okręgu (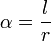 )
) - szybkość kątowa
 bywa równa zakreślonemu kątowi podzielonemu poprzez czas, w jakim został zakreślony. W szczególności, kąt pełny zakreślony bywa w czasie równym okresowi (
bywa równa zakreślonemu kątowi podzielonemu poprzez czas, w jakim został zakreślony. W szczególności, kąt pełny zakreślony bywa w czasie równym okresowi (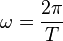 )
) - przyspieszenie dośrodkowe ar równe bywa kwadratowi wartości prędkości podzielonemu poprzez promień; po podstawieniach możemy uzyskać inne wzory (
 )
) - wektor przyspieszenia (
 ) skierowany bywa prostopadle do toru ruchu (okręgu), czyli do środka okręgu; wektor prędkości (
) skierowany bywa prostopadle do toru ruchu (okręgu), czyli do środka okręgu; wektor prędkości ( ) skierowany bywa stycznie do okręgu
) skierowany bywa stycznie do okręgu

 dr inż. Paweł Troka
dr inż. Paweł Troka